题目内容
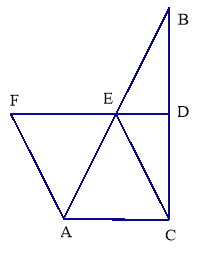
【题目】如图,在△ABC中,∠ACB=90°,BC的垂直平分线DE交BC于D,交AB于E,F在DE上,且AF∥CE.
(1)说明四边形ACEF是平行四边形;(2)当∠B满足什么条件时,四边形ACEF是菱形,并说明理由.
【答案】(1)、证明过程见解析;(2)、∠B=30°;理由见解析
【解析】
试题分析:(1)、根据DE垂直平分BC可得∠EDB=90°,得到DE∥AC,结合AF∥CE得到平行四边形;(2)、根据DE垂直平分BC得到BE=EC,∠B=∠BCE,根据∠B=30°可得∠BCE=30°,∠AEC=60°,根据∠BCA=90°可得∠BAC=60°,则△ACE为正三角形,得到四边形为菱形.
试题解析:(1)、∵ DE垂直平分BC ∴∠EDB=90° ∴ DE∥AC,即FE∥AC
由∵AF∥CE ∴四边形ACEF是平行四边形
(2)、当∠B=30°时,四边形ACEF是菱形
理由:∵DE垂直平分BC ∴BE=EC ∴∠B=∠BCE ∵∠B=30° ∴∠BCE=30°
∴∠AEC=∠B+∠BCE=60° ∵∠BCA=90° ∴∠BAC=90°-∠B=60°
∴△ACE是等边三角形 ∴AC=EC ∵四边形ACEF是平行四边形 ∴四边形ACEF是菱形

练习册系列答案
相关题目