题目内容
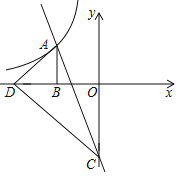
【题目】如图,在平面直角坐标系中,△ABC的顶点在坐标轴上,A,B,C三点的坐标分别为 (0,2),(1,0),(0,-0.5),D为线段AB上-个动点(不与点A,B重合),过B,D,0三点的圆与直线BC交于点E,当△OED面积取得最小值时,ED的长为________.
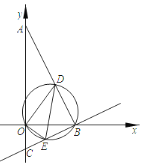
【答案】1
【解析】
如图,先证明△AOB∽△BOC得到∠1=∠2,再判断∠DBE=90°,利用圆周角定理可得到DE为过B,D,O三点的圆的直径,从而得到∠DOE=90°,接着证明△AOD∽△BOE,利用相似比得到OD=2OE,根据三角形面积公式得到S△ODE=OE2,利用垂线段最短判断当△OED面积取得最小值时,OE⊥CB,然后计算OE、OD,最后利用勾股定理计算对应的DE长.
如图,
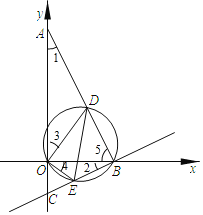
∵A,B,C三点的坐标分别为(0,2),(1,0),(0,-0.5),
∴OA=2,OB=1,OC=![]() ,
,
∵![]() =2,
=2,
而∠AOB=∠BOC,
∴△AOB∽△BOC,
∴∠1=∠2,
∴∠ABC=∠2+∠5=∠1+∠5=90°,
∵∠DBE=90°,
∴DE为过B,D,O三点的圆的直径,
∴∠DOE=90°,
∵∠3+∠BOD=∠4+∠BOD=90°,
∴∠3=∠4,
∵∠1=∠2,
∴△AOD∽△BOE,
∴![]() ,即OD=2OE,
,即OD=2OE,
∵S△ODE=![]() ODOE=
ODOE=![]() 2OEOE=OE2,
2OEOE=OE2,
当△OED面积取得最小值时,OE最小,此时OE⊥CB,
∵BC=![]() ,
,
∴OE=![]() =
=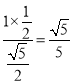 ,
,
此时OD=2OE=![]() ,
,
∴DE=![]() ,
,
即当△OED面积取得最小值时,ED的长为1.
故答案为1.

练习册系列答案
相关题目