题目内容
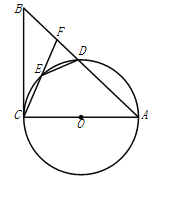
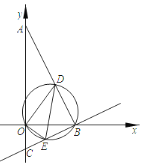
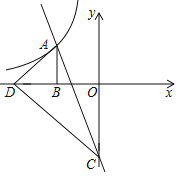
【题目】如图,在平面直角坐标系中,点B在x轴上,∠ABO=90°,AB=BO,直线y=﹣3x﹣4与反比例函数y=![]() 交于点A,交y轴于C点.
交于点A,交y轴于C点.
(1)求k的值;
(2)点D与点O关于AB对称,连接AD、CD,证明△ACD是直角三角形;
(3)在(2)的条件下,点E在反比例函数图象上,若S△OCE=S△OCD,求点E的坐标.
【答案】(1)-4;(2)见解析;(3)点E的坐标为(﹣4,1).
【解析】
(1)根据一次函数图象上点的坐标特征求出点A的坐标,利用待定系数法求出k;
(2)先求出点D的坐标,求出∠ADB=45°,∠ODC=45°,从而得解;
(3)设出点E的坐标,根据三角形的面积公式解答.
(1)设点B的坐标为(a,0),
∵∠ABO=90°,AB=BO,
∴点A的坐标为(a,﹣a),
∵点A在直线y=﹣3x﹣4上,
∴﹣a=﹣3a﹣4,
解得,a=﹣2,
即点A的坐标为(﹣2,2),
∵点A在反比例函数y=![]() 上,
上,
∴k=﹣4;
(2)∵点D与点O关于AB对称,
∴点D的坐标为(﹣4,0)
∴OD=4,
∴DB=BA=2,
则∠ADB=45°,
∵直线y=﹣3x﹣4交y轴于C点,
∴点C的坐标为(0,﹣4),
∴OD=OC,
∴∠ODC=45°,
∴∠ADC=∠ADB+∠ODC=90°,
即△ACD是直角三角形;
(3)设点E的坐标为(m,﹣![]() ),
),
∵S△OCE=S△OCD,
∴![]() ×4×4=
×4×4=![]() ×4×(﹣m),
×4×(﹣m),
解得,m=﹣4,
∴﹣![]() =1,
=1,
∴点E的坐标为(﹣4,1).

练习册系列答案
相关题目