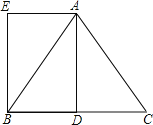ЬтФПФкШн
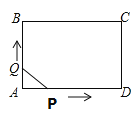
ЁОЬтФПЁПЩшЁїABCЃЌЕуPЪЧЦНУцФкЕФШЮвтвЛЕуЃЈAЁЂBЁЂCШ§ЕуГ§ЭтЃЉЃЌШєЕуPгыЕуAЁЂBЁЂCжаШЮвтСНЕуЕФСЌЯпЕФМаНЧЮЊжБНЧЪБЃЌдђГЦЕуPЮЊЁїABCЕФвЛИіЙДЙЩЕуЃЎ
ЃЈ1ЃЉШчЭМ1ЃЌШєЕуPЪЧЁїABCФквЛЕуЃЌЁЯAЃН50ЁуЃЌЁЯACPЃН10ЁуЃЌЁЯABPЃН30ЁуЃЌЪдЫЕУїЕуPЪЧЁїABCЕФвЛИіЙДЙЩЕуЃЎ
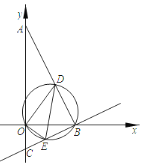
ЃЈ2ЃЉШчЭМ2ЃЌRtЁїABCжаЃЌЁЯACBЃН90ЁуЃЌACЃН6ЃЌBCЃН8ЃЌЕуDЪЧABЕФжаЕуЃЌЕуPдкЩфЯпCDЩЯЃЌШєЕуPЪЧЁїABCЕФЙДЙЩЕуЃЌдђCPЃНЁЁ ЁЁЃЛ
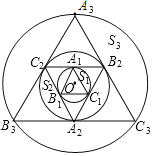
ЃЈ3ЃЉШчЭМ3ЃЌЫФБпаЮABDCжаЃЌDBЃНDAЃЌЁЯBCDЃН45ЁуЃЌACЃН![]() ЃЌCDЃН3ЃЎдђЕуDФмЗёЪЧЁїABCЕФЙДЙЩЕуЃЌШєФмЃЌЧѓГіBCЕФГЄЃКШєВЛФмЃЌЧыЫЕУїРэгЩЃЎ
ЃЌCDЃН3ЃЎдђЕуDФмЗёЪЧЁїABCЕФЙДЙЩЕуЃЌШєФмЃЌЧѓГіBCЕФГЄЃКШєВЛФмЃЌЧыЫЕУїРэгЩЃЎ

ЁОД№АИЁП(1)МћНтЮіЃЛЃЈ2ЃЉ![]() Лђ
Лђ![]() Лђ10ЃЛЃЈ3ЃЉЕуDПЩвдЪЧЁїABCЕФЙДЙЩЕуЃЌBCЕФГЄЪЧ
Лђ10ЃЛЃЈ3ЃЉЕуDПЩвдЪЧЁїABCЕФЙДЙЩЕуЃЌBCЕФГЄЪЧ![]()
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЙДЙЩЕуЕФЖЈвхПЩЕУНсТлЃЛ
ЃЈ2ЃЉШєЕуPЪЧЁїABCЕФЙДЙЩЕуЃЌгаШ§жжЧщПіЃКЂйЕБЁЯAPCЃН90ЁуЪБЃЌЂкЕБЁЯBPCЃН90ЁуЪБЃЌЂлЕБЁЯAPBЃН90ЁуЪБЃЌЗжБ№ИљОнSЁїACDЃН![]() SЁїABCКЭжБНЧШ§НЧаЮаББпжаЯпЕФаджЪНјааМЦЫуМДПЩЃЛ
SЁїABCКЭжБНЧШ§НЧаЮаББпжаЯпЕФаджЪНјааМЦЫуМДПЩЃЛ
ЃЈ3ЃЉДцдкЃЌЕБЁЯADBЃН90ЁуЪБЃЌЕуDЪЧЁїABCЕФЙДЙЩЕуЃЌШчЭМ5ЃЌзїИЈжњЯпЃЌЙЙНЈжБНЧШ§НЧаЮЃЌжЄУїЁїAEDЁеЁїDFBЃЈAASЃЉЃЌЕУAEЃНDFЃЌИљОнЕШбќжБНЧШ§НЧаЮМЦЫуAEЕФГЄЃЌПЩЕУDFЕФГЄЃЌПЩЕУНсТлЃЎ
ЃЈ1ЃЉЁпЁЯAЃН50ЁуЃЌЁЯACPЃН10ЁуЃЌЁЯABPЃН30ЁуЃЌ
ЁрЁЯPCB+ЁЯPBCЃН180ЁуЉ50ЁуЉ10ЁуЉ30ЁуЃН90ЁуЃЌ
ЁрЁЯBPCЃН90ЁуЃЌ
ЁрЕуPЪЧЁїABCЕФвЛИіЙДЙЩЕуЃЛ
ЃЈ2ЃЉЕуPдкЩфЯпCDЩЯЃЌШєЕуPЪЧЁїABCЕФЙДЙЩЕуЃЌДцдквдЯТШ§жжЧщПіЃК
ЂйШчЭМ2ЃЌЕБЁЯAPCЃН90ЁуЪБЃЌACЃН6ЃЌBCЃН8ЃЌ
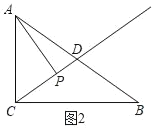
ЁрABЃН10ЃЌ
ЁпDЪЧABЕФжаЕуЃЌ
ЁрCDЃН![]() ABЃН5ЃЌ
ABЃН5ЃЌ
SЁїACDЃН![]() SЁїABCЃН
SЁїABCЃН![]() CDAPЃЌ
CDAPЃЌ
![]() ЃЌ
ЃЌ
APЃН![]() ЃЌ
ЃЌ
Ёр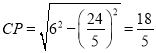 ЃЛ
ЃЛ
ЂкШчЭМ3ЃЌЕБЁЯBPCЃН90ЁуЪБЃЌ
SЁїACDЃН![]() SЁїABCЃН
SЁїABCЃН![]() CDBPЃЌ
CDBPЃЌ
![]() ЃЌ
ЃЌ
BPЃН![]() ЃЌ
ЃЌ
ЁрCPЃН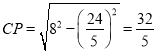 ЃЛ
ЃЛ
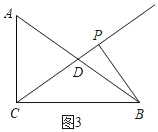
ЂлШчЭМ4ЃЌЕБЁЯAPBЃН90ЁуЪБЃЌ
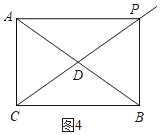
ЁпDЪЧABЕФжаЕуЃЌ
ЁрPDЃН![]() ABЃН5ЃЌ
ABЃН5ЃЌ
ЁрPCЃН5+5ЃН10ЃЌ
злЩЯЃЌPCЕФГЄЪЧ![]() Лђ
Лђ![]() Лђ10ЃЛ
Лђ10ЃЛ
ЙЪД№АИЮЊЃК![]() Лђ
Лђ![]() Лђ10ЃЛ
Лђ10ЃЛ
ЃЈ3ЃЉДцдкЃЌ
ЕБЁЯADBЃН90ЁуЪБЃЌЕуDЪЧЁїABCЕФЙДЙЩЕуЃЌШчЭМ5ЃЌЙ§AзїAEЁЭCDЃЌНЛжБЯпCDгкEЃЌЙ§BзїBFЁЭCDгкFЃЌ
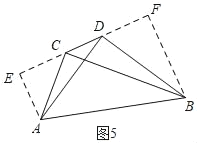
ЁпЁЯADBЃНЁЯADE+ЁЯBDFЃНЁЯBDF+ЁЯDBFЃН90ЁуЃЌ
ЁрЁЯADEЃНЁЯDBFЃЌ
ЁпЁЯEЃНЁЯFЃН90ЁуЃЌADЃНBDЃЌ
ЁрЁїAEDЁеЁїDFBЃЈAASЃЉЃЌ
ЁрAEЃНDFЃЌ
ЁпADЃНBDЃЌ
ЁрЁїADBЪЧЕШбќжБНЧШ§НЧаЮЃЌ
ЁрЁЯDABЃН45ЁуЃЌ
ЁпЁЯBCDЃН45ЁуЃЌ
ЁрЁЯBCDЃНЁЯDABЃЌ
ЁрAЁЂBЁЂDЁЂCЫФЕуЙВдВЃЌ
ЁрЁЯACBЃНЁЯADBЃН90ЁуЃЌ
ЁрЁЯACEЃН45ЁуЃЌ
ЁпACЃН![]() ЃЌ
ЃЌ
ЁрAEЃНCEЃНDFЃН![]() ЃЌ
ЃЌ
ЁрCF![]() ЃЌ
ЃЌ
ЁрBCЃН![]() CEЃН
CEЃН![]() ЃЛ
ЃЛ
злЩЯЃЌЕуDПЩвдЪЧЁїABCЕФЙДЙЩЕуЃЌBCЕФГЄЪЧ![]() ЃЎ
ЃЎ

ЁОЬтФПЁПМЦЫуФмСІЪЧЪ§бЇЕФЛљБОФмСІЃЌЮЊСЫНјвЛВНСЫНтбЇЩњЕФМЦЫуЧщПіЃЌГѕ2020МЖЪ§бЇРЯЪІУЧЖдФГДЮПМЪджаЕк19ЬтМЦЫуЬтЕФЕУЗжЧщПіНјааСЫЕїВщЃЌЯжЗжБ№ДгAЁЂBСНАрЫцЛњИїГщШЁ10УћбЇЩњЕФГЩМЈШчЯТЃК
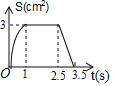
AАр10УћбЇЩњЕФГЩМЈЛцГЩСЫЬѕаЮЭГМЦЭМЃЌШчЯТЭМЃЌ

BАр10УћбЇЩњЕФГЩМЈЃЈЕЅЮЛЃКЗжЃЉЗжБ№ЮЊЃК9ЃЌ8ЃЌ9ЃЌ10ЃЌ9ЃЌ7ЃЌ9ЃЌ8ЃЌ10ЃЌ8
ОЙ§РЯЪІЖдЫљГщШЁбЇЩњГЩМЈЕФећРэгыЗжЮіЃЌЕУЕНСЫШчЯТБэЪ§ОнЃК
AАр | BАр | |
ЦНОљЪ§ | 8.3 | a |
жаЮЛЪ§ | b | 9 |
жкЪ§ | 8Лђ10 | c |
МЋВю | 4 | 3 |
ЗНВю | 1.81 | 0.81 |
ИљОнвдЩЯаХЯЂЃЌНтД№ЯТСаЮЪЬтЃЎ
ЃЈ1ЃЉВЙШЋЬѕаЮЭГМЦЭМЃЛ
ЃЈ2ЃЉжБНгаДГіБэжаaЃЌbЃЌcЕФжЕЃКaЃНЁЁ ЁЁЃЌbЃНЁЁ ЁЁЃЌcЃНЁЁ ЁЁЃЛ
ЃЈ3ЃЉИљОнвдЩЯЪ§ОнЃЌФуШЯЮЊAЁЂBСНИіАрФФИіАрМЦЫуЬтеЦЮеЕУИќКУЃПЧыЫЕУїРэгЩЃЈаДГіЦфжаСНЬѕМДПЩЃЉЃКЁЁ ЁЁЃЎ
ЃЈ4ЃЉШє9ЗжМА9ЗжвдЩЯЮЊгХауЃЌШєAАрЙВ55ШЫЃЌдђAАрМЦЫуЬтгХауЕФДѓдМгаЖрЩйШЫЃП