Question

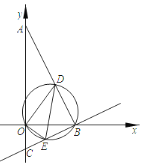
【题目】如图，四边形ABCD中AB＝BC＝CD＝AD，∠BAD＝90°，对角线AC、BD相交于点O．

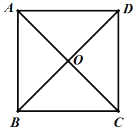
（1）求证：四边形ABCD是正方形；

（2）若P是对角线BD上任意一点，连接PA，PA绕点P逆时针旋转90°得到PE，连接AE、BE．

①根据题意画图，判断B、C、E三点是否共线，并说明理由；

②当BD＝8，△PBE的面积等于时，求PB的长

Answer 1

【答案】（1）见解析；（2）①B、C、E三点共线，见解析；②PB为1或3或

【解析】

（1）根据正方形的判定定理证明；

（2）①根据题意画出图形；根据旋转的性质得到△APE为等腰直角三角形，根据正方形的性质得到△AOB为等腰直角三角形，证明△AOP∽△ABE，根据相似三角形的性质得到∠ABE=90°，得到答案；

②根据题意求出OB，根据相似三角形的性质得到BE=（4-PB），求出PH，根据三角形的面积公式列式计算．

解：（1）∵AB＝BC＝CD＝AD，

∴四边形ABCD是菱形；

∵∠BAD＝90°，

∴四边形ABCD是正方形；

（2）①如图，就是所画的图形 （图②或图③）结论：B、C、E三点共线.

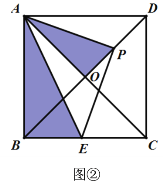
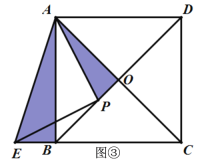
理由：由画图得，PA＝PE，PA⊥PE，

∴∠PAE＝∠PEA＝45°，

由（1）得四边形ABCD是正方形，

∴AC⊥BD，OA＝OB

∴∠OAB＝∠OBA＝45°，

∴∠PAE＝∠OAB，∠PEA＝∠OBA，

∴△PAE∽△OAB，

∴，

∵∠PAE＝∠OAB，

∴∠PAO＝∠EAB，

∴△PAO∽△EAB

∴∠POA＝∠EBA＝90°，

∴AB⊥BE，

∵∠ABC＝90°，

∴AB⊥BC，

∴B、C、E三点共线；

②分两种情况讨论：

当点P在线段OD上时，作PF⊥BC，如图④，

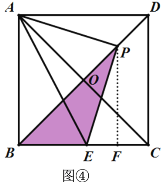
由（1）得四边形ABCD是正方形，

∵AC＝BD＝8

∴AO＝B0＝4，AB＝

设PB＝x，则PO＝ x－4，

由①得△PAO∽△EAB，

∴，

∴

∴

由（1）得四边形ABCD是正方形，且PF⊥BC，

得△PBF为等腰直角三角形，

∴PF＝

∴S＝（4≤x≤8），

解得，（舍去）；

当点P在线段BO上时，作PE⊥BD，如图⑤，

由（1）得四边形ABCD是正方形，

∵AC＝BD＝8

∴AO＝B0＝4，AB＝

设PB＝x，则PO＝4－x，

由①得△PAO∽△EAB，

∴，

∴

∴

由（1）得四边形ABCD是正方形，且PF⊥BC，

得△PBF为等腰直角三角形，

∴PF＝

∴S＝（0≤x＜4），

解得，；

综上所述，当PB为1或3或时，△PBE的面积等于．