题目内容
【题目】如图，在□ABCD中，BE平分∠ABC交AD于点E，DF平分∠ADC交BC于点F．
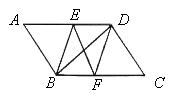
【1】△ABE≌△CDF
【2】若BD⊥EF，则判断四边形EBFD是什么特殊四边形，请证明你的结论．
【答案】
【1】∵四边形
是平行四边，∴
∵
平分
平分
∴
……………3分
∴
…………………………………………4分
【2】由
得
…………………………………5分
在平行四边形中，
∴
∴四边形
是平行四边形…………………………………………7分
若
则四边形是菱形…………………………………8分
【解析】（1）由平行四边形ABCD可得出的条件有：①AB=CD，②∠A=∠C，③∠ABC=∠CDA；已知BE、CD分别是等角∠ABD、∠CDA的平分线，易证得∠ABE=∠CDF④；联立①②④，即可由ASA判定所求的三角形全等；
（2）由（1）的全等三角形，易证得DE=BF，那么DE和BF平行且相等，由此可判定四边形BEDF是平行四边形，根据对角线垂直的平行四边形是菱形即可得出EBFD的形状．
练习册系列答案
相关题目
【题目】有这样一个问题:探究函数
的图象与性质.
小亮根据学习函数的经验，对函数的图象与性质进行了探究。
下面是小亮的探究过程，请补充完整:
(1)函数中自变量x的取值范围是_________.
(2)下表是y与x的几组对应值.
x | … | -3 | -2 | -1 | 0 |
|
| 2 | 3 | 4 | 5 | … |
y | … | - | - | -4 | -5 | -7 | m | -1 | -2 | - | - | … |
求m的值；
(3)在平面直角坐标系xOy中，描出了以上表中各对对应值为坐标的点，根据描出的点，画出该函数的图象；
(4)根据画出的函数图象，发现下列特征:该函数的图象与直线x=1越来越靠近而永不相交，该函数的图象还与直线_________越来越靠近而永不相交.
