ЬтФПФкШн
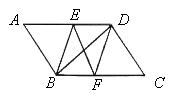
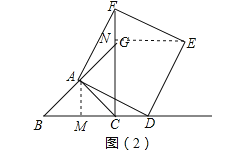
ЁОЬтФПЁПдкЁїABCжаЃЌAB=ACЃЌЁЯBAC=90ЁуЃЌЕуDдкЩфЯпBCЩЯЃЈгыBЁЂCСНЕуВЛжиКЯЃЉЃЌвдADЮЊБпзїе§ЗНаЮADEFЃЌЪЙЕуEгыЕуBдкжБЯпADЕФвьВрЃЌЩфЯпBAгыжБЯпCFЯрНЛгкЕуGЃЎ
ЃЈ1ЃЉШєЕуDдкЯпЖЮBCЩЯЃЌШчЭМЃЈ1ЃЉЃЌХаЖЯЃКЯпЖЮBCгыЯпЖЮCGЕФЪ§СПЙиЯЕЃКЁЁ ЁЁЃЌЮЛжУЙиЯЕЃКЁЁ ЁЁЃЎ
ЃЈ2ЃЉШчЭМЃЈ2ЃЉЃЌЂйШєЕуDдкЯпЖЮBCЕФбгГЄЯпЩЯЃЌЃЈ1ЃЉжаХаЖЯЯпЖЮBCгыЯпЖЮCGЕФЪ§СПЙиЯЕгыЮЛжУЙиЯЕЪЧЗёШдШЛГЩСЂЃЌВЂЫЕУїРэгЩЃЛ
ЂкЕБGЮЊCFжаЕуЃЌСЌНгGEЃЌШєAB=![]() ЃЌЧѓЯпЖЮGEЕФГЄЃЎ
ЃЌЧѓЯпЖЮGEЕФГЄЃЎ
ЁОД№АИЁП(1) BC=CGЃЌBCЁЭCG (2) ЂйШдШЛГЩСЂ Ђк![]()
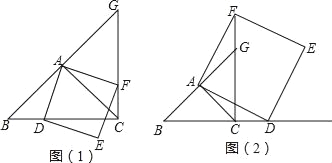
ЁОНтЮіЁПЗжЮіЃКЃЈ1ЃЉИљОнЕШбќжБНЧШ§НЧаЮЕФаджЪЕУЕНЁЯACB=ЁЯABC=45ЁуЃЌгЩе§ЗНаЮЕФаджЪЕУЕНAD=AFЃЌЁЯDAF=90ЁуЃЌгЩНЧЕФКЭВюЕУЕНЁЯBAD=ЁЯCAFЃЌЭЦГіЁїBADЁеЁїCAFЃЈSASЃЉЃЌИљОнШЋЕШШ§НЧаЮЕФаджЪЕУЕНЁЯACF=ЁЯB=45ЁуЃЌBD=CFЃЌжЄЕУBCЁЭCGЃЌЭЌРэЁїADCЁеЁїAFGЃЌМДПЩЕУЕННсТлЃЛ
ЃЈ2ЃЉЂйИљОнЕШбќжБНЧШ§НЧаЮЕФаджЪЕУЕНЁЯACB=ЁЯABC=45ЁуЃЌгЩе§ЗНаЮЕФаджЪЕУЕНAD=AFЃЌЁЯDAF=90ЁуЃЌгЩНЧЕФКЭВюЕУЕНЁЯBAD=ЁЯCAFЃЌЭЦГіЁїBADЁеЁїCAFЃЈSASЃЉЃЌИљОнШЋЕШШ§НЧаЮЕФаджЪЕУЕНЁЯACF=ЁЯB=45ЁуЃЌBD=CFЃЌжЄЕУBCЁЭCGЃЌЭЌРэЁїADCЁеЁїAFGЃЌМДПЩЕУЕННсТлЃЛЂкгыЂйЭЌРэЃЌПЩЕУBD=CFЃЌBC=CGЃЌBCЁЭCGЃЌИљОнвбжЊЬѕМўЕУЕНBC=CG=FG=CD=2ЃЌШчЭМЃЈ2ЃЉЃЌЙ§ЕуAзїAMЁЭBDгкMЃЌИљОнЙДЙЩЖЈРэЕУЕНAD=![]() ЃЌЙ§ЕуEзїENЁЭFGгкNЃЌИљОнШЋЕШШ§НЧаЮЕФаджЪЕУЕНFG=AM=1ЃЌЭЦГіNEЮЊFGЕФДЙжБЦНЗжЯпЃЌМДПЩЕУЕННсТлЃЎ
ЃЌЙ§ЕуEзїENЁЭFGгкNЃЌИљОнШЋЕШШ§НЧаЮЕФаджЪЕУЕНFG=AM=1ЃЌЭЦГіNEЮЊFGЕФДЙжБЦНЗжЯпЃЌМДПЩЕУЕННсТлЃЎ
ЯъНтЃКЃЈ1ЃЉBC=CGЃЌBCЁЭCGЃЎ
ЁпЁЯBAC=90ЁуЃЌAB=ACЃЌЁрЁЯACB=ЁЯABC=45ЁуЃЎ
ЁпЫФБпаЮADEFЪЧе§ЗНаЮЃЌЁрAD=AFЃЌЁЯDAF=90ЁуЃЎ
ЁпЁЯBAD=90ЁуЉЁЯDACЃЌЁЯCAF=90ЁуЉЁЯDACЃЌЁрЁЯBAD=ЁЯCAFЃЌдђдкЁїBADКЭЁїCAFжаЃЌ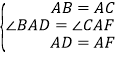 ЃЌЁрЁїBADЁеЁїCAFЃЈSASЃЉЃЌЁрЁЯACF=ЁЯB=45ЁуЃЌBD=CFЃЌЁрЁЯBCF=ЁЯACB+ЁЯACF=90ЁуЃЌЁрBCЁЭCGЃЌЭЌРэЁїADCЁеЁїAFGЃЌЁрCD=GFЃЌЁрBD+CD=CF+GFЃЌМДBC=CGЃЎ
ЃЌЁрЁїBADЁеЁїCAFЃЈSASЃЉЃЌЁрЁЯACF=ЁЯB=45ЁуЃЌBD=CFЃЌЁрЁЯBCF=ЁЯACB+ЁЯACF=90ЁуЃЌЁрBCЁЭCGЃЌЭЌРэЁїADCЁеЁїAFGЃЌЁрCD=GFЃЌЁрBD+CD=CF+GFЃЌМДBC=CGЃЎ
ЙЪД№АИЮЊЃКBC=CGЃЌBCЁЭCGЃЛ
ЃЈ2ЃЉЂйШдШЛГЩСЂ
ЁпЫФБпаЮADEFЪЧе§ЗНаЮЃЌЁрAD=AFЃЌЁЯDAF=90ЁуЃЎ
ЁпЁЯBAD=90ЁуЉЁЯDACЃЌЁЯCAF=90ЁуЉЁЯDACЃЌЁрЁЯBAD=ЁЯCAFЃЌдђдкЁїBADКЭЁїCAFжаЃЌ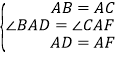 ЃЌЁрЁїBADЁеЁїCAFЃЈSASЃЉЃЌЁрЁЯACF=ЁЯB=45ЁуЃЌBD=CFЃЌЁрЁЯBCF=ЁЯACB+ЁЯACF=90ЁуЃЌЁрBCЁЭCGЃЌЭЌРэЁїADCЁеЁїAFGЃЌЁрCD=GFЃЌЁрBD+CD=CF+GFЃЌМДBC=CGЃЛ
ЃЌЁрЁїBADЁеЁїCAFЃЈSASЃЉЃЌЁрЁЯACF=ЁЯB=45ЁуЃЌBD=CFЃЌЁрЁЯBCF=ЁЯACB+ЁЯACF=90ЁуЃЌЁрBCЁЭCGЃЌЭЌРэЁїADCЁеЁїAFGЃЌЁрCD=GFЃЌЁрBD+CD=CF+GFЃЌМДBC=CGЃЛ
ЂкгыЂйЭЌРэЃЌПЩЕУBD=CFЃЌBC=CGЃЌBCЁЭCGЃЎ
ЁпAB=![]() ЃЌGЮЊCFжаЕуЃЌЁрBC=CG=FG=CD=2ЃЌШчЭМЃЈ2ЃЉЃЌЙ§ЕуAзїAMЁЭBDгкMЃЌЁрAM=1ЃЌMD=3ЃЌЁрAD=
ЃЌGЮЊCFжаЕуЃЌЁрBC=CG=FG=CD=2ЃЌШчЭМЃЈ2ЃЉЃЌЙ§ЕуAзїAMЁЭBDгкMЃЌЁрAM=1ЃЌMD=3ЃЌЁрAD=![]() ЃЌЙ§ЕуEзїENЁЭFGгкNЃЎдкЁїAMDгыЁїFNEжаЃЌ
ЃЌЙ§ЕуEзїENЁЭFGгкNЃЎдкЁїAMDгыЁїFNEжаЃЌ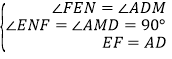 ЃЌЁрЁїAMDЁеЁїFNEЃЌЁрFN=AM=1ЃЌЁрFG=2FNЃЌЁрNEЮЊFGЕФДЙжБЦНЗжЯпЃЌМДGE=FE=AD=
ЃЌЁрЁїAMDЁеЁїFNEЃЌЁрFN=AM=1ЃЌЁрFG=2FNЃЌЁрNEЮЊFGЕФДЙжБЦНЗжЯпЃЌМДGE=FE=AD=![]() ЃЎ
ЃЎ

 ЧсЫЩПЮЬУЕЅдЊЦкжаЦкФЉзЈЬтГхДЬ100ЗжЯЕСаД№АИ
ЧсЫЩПЮЬУЕЅдЊЦкжаЦкФЉзЈЬтГхДЬ100ЗжЯЕСаД№АИ