ЬтФПФкШн
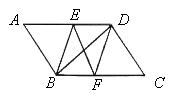
ЁОЬтФПЁПдкСтаЮABCDжаЃЌЁЯABCЃН60ЁуЃЌPЪЧЩфЯпBDЩЯвЛЖЏЕуЃЌвдAPЮЊБпЯђгвВрзїЕШБпЁїAPEЃЌСЌНгCEЃЎ
ЃЈ1ЃЉШчЭМ1ЃЌЕБЕуPдкСтаЮABCDФкВПЪБЃЌдђBPгыCEЕФЪ§СПЙиЯЕЪЧЁЁ ЁЁЃЌCEгыADЕФЮЛжУЙиЯЕЪЧЁЁ ЁЁЃЎ
ЃЈ2ЃЉШчЭМ2ЃЌЕБЕуPдкСтаЮABCDЭтВПЪБЃЌЃЈ1ЃЉжаЕФНсТлЪЧЗёЛЙГЩСЂЃПШєГЩСЂЃЌЧыгшвджЄУїЃЛШєВЛГЩСЂЃЌЧыЫЕУїРэгЩЃЛ
ЃЈ3ЃЉШчЭМ2ЃЌСЌНгBEЃЌШєABЃН2![]() ЃЌBEЃН2
ЃЌBEЃН2![]() ЃЌЧѓAPЕФГЄЃЎ
ЃЌЧѓAPЕФГЄЃЎ

ЁОД№АИЁПЃЈ1ЃЉBP=CEЃЌCEЁЭADЃЛЃЈ2ЃЉНсТлШдШЛГЩСЂЃЌРэгЩМћНтЮіЃЛЃЈ3ЃЉ2![]()
ЁОНтЮіЁП
ЃЈ1ЃЉгЩСтаЮABCDКЭЁЯABC=60ЁуПЩжЄЁїABCгыЁїACDЪЧЕШБпШ§НЧаЮЃЌгЩЕШБпЁїAPEПЩЕУAP=AEЃЌЁЯPAE=ЁЯBAC=60ЁуЃЌМѕШЅЙЋЙВНЧЁЯPACЕУЁЯBAP=ЁЯCAEЃЌИљОнSASПЩжЄЕУЁїBAPЁеЁїCAEЃЌЙЪгаBP=CEЃЌЁЯABP=ЁЯACEЃЎгЩСтаЮЖдНЧЯпЦНЗжвЛзщЖдНЧПЩжЄЁЯABP=30ЁуЃЌЙЪЁЯACE=30ЁуМДCEЦНЗжЁЯACDЃЌгЩAC=CDЕШбќШ§НЧаЮШ§ЯпКЯвЛПЩЕУCEЁЭADЃЎ
ЃЈ2ЃЉНсТлВЛБфЃЎжЄУїЙ§ГЬЭЌЃЈ1ЃЉЃЎ
ЃЈ3ЃЉдкRtЁїAOPжаЃЌЧѓГіOAЃЌOPМДПЩНтОіЮЪЬтЃЎ
ЃЈ1ЃЉBP=CEЃЌCEЁЭADЃЎ
РэгЩЃКЁпСтаЮABCDжаЃЌЁЯABC=60Ёу
ЁрAB=BC=CD=ADЃЌЁЯADC=ЁЯABC=60Ёу
ЁрЁїABCЁЂЁїACDЪЧЕШБпШ§НЧаЮ
ЁрAB=ACЃЌAC=CDЃЌЁЯBAC=ЁЯACD=60Ёу
ЁпЁїAPEЪЧЕШБпШ§НЧаЮ
ЁрAP=AEЃЌЁЯPAE=60Ёу
ЁрЁЯBAC-ЁЯPAC=ЁЯPAE-ЁЯPAC
МДЁЯBAP=ЁЯCAEЃЌ
ЁрЁїBAPЁеЁїCAEЃЈSASЃЉ
ЁрBP=CEЃЌЁЯABP=ЁЯACE
ЁпBDЦНЗжЁЯABC
ЁрЁЯACE=ЁЯABP=![]() ЁЯABC=30Ёу
ЁЯABC=30Ёу
ЁрCEЦНЗжЁЯACD
ЁрCEЁЭADЃЎ
ЙЪД№АИЮЊBP=CEЃЌCEЁЭADЃЎ
ЃЈ2ЃЉНсТлШдШЛГЩСЂЃЎРэгЩШчЯТЃКШчЭМЃЌЩшCEНЛADгкHЃЌСЌНгACЃЎ
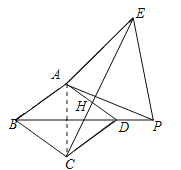
ЁпЫФБпаЮABCDЪЧСтаЮЃЌЁЯABC=60ЁуЃЌ
ЁрЁїABCЃЌЁїACDЖМЪЧЕШБпШ§НЧаЮЃЌЁЯABD=ЁЯCBD=30ЁуЃЎ
ЁпЁїAPEЪЧЕШБпШ§НЧаЮЃЌ
ЁрAB=ACЃЌAP=AEЃЌЁЯBAC=ЁЯPAE=60ЁуЃЎ
ЁрЁїBAPЁеЁїCAEЃЎ
ЁрBP=CEЃЌЁЯABP=ЁЯACE=30ЁуЃЎ
ЁпЁЯCAH=60ЁуЃЌ
ЁрЁЯCAH+ЁЯACH=90ЁуЃЎ
ЁрЁЯAHC=90ЁуЃЌМДCEЁЭADЃЎ
ЃЈ3ЃЉШчЭМЃЌСЌНгBEЃЌ
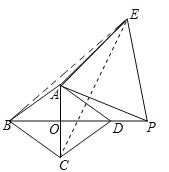
гЩЃЈ2ЃЉПЩжЊCEЁЭADЃЌBP= CEЃЎ
дкСтаЮABCDжаЃЌADЁЮBCЃЌЁрCEЁЭBCЃЎ
ЁпBC=AB=2![]() ЃЌBE=2
ЃЌBE=2![]() ЃЌ
ЃЌ
дкRtЁїBCEжаЃЌCE=![]() =8ЃЎ
=8ЃЎ
ЁрBP=CE=8ЃЎ
ЁпACгыBDЪЧСтаЮЕФЖдНЧЯпЃЌ
ЁрЁЯABD=![]() ЁЯABC=30ЁуЃЌACЁЭBDЃЎ
ЁЯABC=30ЁуЃЌACЁЭBDЃЎ
ЁрOA=![]() AB=
AB=![]() ЃЌBO=
ЃЌBO=![]() =3ЃЌ
=3ЃЌ
ЁрOP=BPЃBO=5ЃЌ
дкRtЁїAOPжаЃЌAP=![]() =2
=2![]() ЃЌ
ЃЌ

 ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ
ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ