题目内容
【题目】下面是小明设计的“作矩形ABCD”的尺规作图过程:已知:在Rt△ABC中,∠ABC=90°.求作:矩形ABCD.
作法:如图

①以点B为圆心,AC长为半径作弧;
②以点C为圆心,AB长为半径作弧;
③两弧交于点D,A,D在BC同侧;
④连接AD,CD.
所以四边形ABCD是矩形,
根据小明设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:链接BD.
∵AB=________,AC=__________,BC=BC
∴ΔABC≌ΔDCB
∴∠ABC=∠DCB=90°
∴AB∥CD.
∴四边形ABCD是平行四边形
∵∠ABC=90°
∴四边形ABCD是矩形.(_______________)(填推理的依据)
【答案】(1)见解析;(2)CD,BD,有一个角是直角的平行四边形是矩形
【解析】
(1)根据作法画出对应的几何图形即可;
(2)先利用作图证明△ABC≌△DCB,得AB∥CD,根据一组对边平行且相等的四边形是平行四边形,由有一个角是直角的平行四边形是矩形可得结论.
解:(1)如图1,四边形ABCD为所作;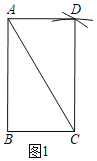
(2)完成下面的证明: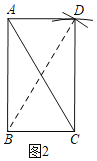
证明:如图2,连接BD.
∵AB=CD,AC=BD,BC=BC,
∴△ABC≌△DCB(SSS).
∴∠ABC=∠DCB=90°.
∴AB∥CD.
∴四边形ABCD是平行四边形.
∵∠ABC=90°
∴四边形ABCD是矩形.(有一个角是直角的平行四边形是矩形)
故答案为:CD,BD,有一个角是直角的平行四边形是矩形.

练习册系列答案
相关题目