题目内容
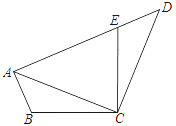
【题目】把长方形 ![]() 沿对角形线AC折叠,得到如图所示的图形,已知∠BAO=30°,
沿对角形线AC折叠,得到如图所示的图形,已知∠BAO=30°,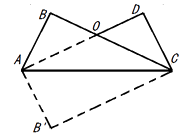
(1)求∠AOC和∠BAC的度数;
(2)若AD= ![]() ,OD=
,OD= ![]() ,求CD的长
,求CD的长
【答案】
(1)解:∵四边形 ![]() 是矩形
是矩形
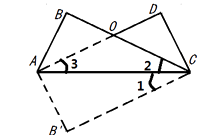
∴AD∥ ![]() ,
, ![]()
∴∠1=∠3
∵翻折后∠1=∠2
∴∠2=∠3
∵翻折后 ![]()
∠BAO=30°
∴ ![]()
∴∠2=∠3=30°
∴ ![]()
(2)解:∵∠2=∠3
∴AO=CO
∵AD= ![]() ,OD=
,OD= ![]()
∴AO=CO= ![]()
∵四边形 ![]() 是矩形
是矩形
∴∠D是直角
∴在 ![]() 中,
中, ![]()
【解析】(1)根据矩形的性质及折叠的性质证出∠2=∠3,再根据∠BAO=30°及∠B=90°,得出∠3的度数,根据三角形的内角和定理求出∠AOC的度数;然后根据直角三角形两锐角互余得出∠BAC的度数即可。
(2)已证得∠2=∠3得出AO=CO,根据已知易求出CO的长,再根据勾股定理,在Rt△ODC中求出CD的长即可。

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目