Question

【题目】甲、乙两人在某标准游泳池相邻泳道进行100米自由泳训练，如图是他们各自离出发点的距离y（米）与他们出发的时间x（秒）的函数图象．根据图象，解决如下问题．（注标准泳池单向泳道长50米，100米自由泳要求运动员在比赛中往返一次；返回时触壁转身的时间，本题忽略不计）.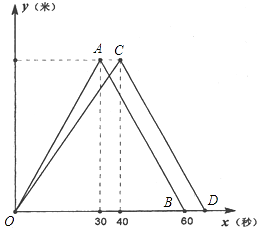

（1）直接写出点A坐标，并求出线段OC的解析式；
（2）他们何时相遇？相遇时距离出发点多远？
（3）若甲、乙两人在各自游完50米后，返回时的速度相等；则快者到达终点时领先慢者多少米？

Answer 1

【答案】
（1）解：由图得点A（30，50），C（40，50），

设线段OC的解析式为：y1=k1x，

把点C（40，50）代入得， ，

∴线段OC的解析式为：y1= （0≤x≤40）

（2）解：设线段AB的解析式为y2=k2x+b，

把点A（30，50）、点B（60，0）代入可知：

解得， ，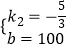

∴线段AB的解析式为y2= ，（30≤x≤60）；

解方程组 ，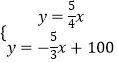

解得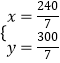， ，∴线段OC与线段AB的交点为（ ， ），

即出发 秒后相遇，相遇时距离出发点 米

（3）解：∵甲乙两人在各自游完50米后，在返程中的距离保持不变，

把x=30代入y1= ，得y1= 米，

把x=40代入y2= ，得y2= 米，

∴快者到达终点时，领先慢者 米

【解析】 （1）观察图像易得出点A的坐标，线段OC是正比例函数，设函数解析式，再将点C的坐标代入即可得出结果。
（2）先根据点A、B的坐标求出直线AB的函数解析式，再将直线AB和直线CD联立方程组，解方程组，即可得出两直线的交点坐标，根据交点坐标即可得出结果。
（3）将x=30和x=40分别代入y1和y2，即可求出快者到达终点时，领先慢者的路程。