题目内容
【题目】如图,在平面直角坐标系中,一次函数y=-x+b的图象与正比例函数y=kx的图象都经过点B(3,1)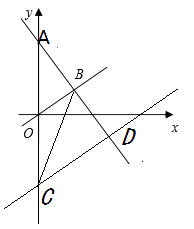
(1)求一次函数和正比例函数的表达式;
(2)若直线CD与正比例函数y=kx平行,且过点C(0,-4),与直线AB相交于点D,求点D的坐标.(注:二直线平行, ![]() 相等)
相等)
(3)连接CB,求三角形BCD的面积.
【答案】
(1)解:把B(3,1)分别代入y=-x+b和y=kx得
![]() ,
, ![]()
解之得: ![]() ,
, ![]()
∴ ![]() ,
, ![]()
(2)解:∵二直线平行,CD经过C(0,-4)
∴直线CD为 ![]()
由题意得: 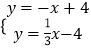
解之得 ![]()
∴点D为(6,-2)
(3)解:易得A(0,4)
∴AC=8
∴ ![]()
【解析】(1)利用待定系数法,将点B的坐标分别代入两函数解析式,建立方程求解,即可两函数解析式。
(2)根据两直线平行k值相等,就可以求出直线CD函数解析式,再将两函数解析式联立方程组,解方程组,求解即可得出交点D的坐标。
(3)先求出点A的坐标,再根据S△BCD=S△ACD-S△ABC。计算即可求出结果。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
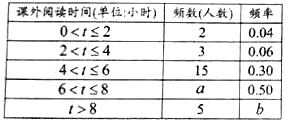
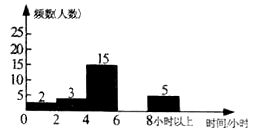
【题目】“莲城读书月”活动结束后,对八年级(三)班45人所阅读书籍数量情况的统计结果如下表所示:
阅读数量 | 1本 | 2本 | 3本 | 3本以上 |
人数(人) | 10 | 18 | 13 | 4 |
根据统计结果,阅读2本书籍的人数最多,这个数据2是( )
A.平均数 B.中位数 C.众数 D.方差