Question

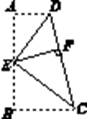
【题目】如图，已知：在四边形ABCD中，点E在AD上，∠BCE＝∠ACD＝90°，∠BAC＝∠D ， BC＝CE ．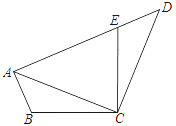

（1）求证：AC＝CD；
（2）若AC＝AE ， 求∠DEC的度数．

Answer 1

【答案】
（1）解：证明：

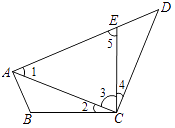
在△ABC和△DEC中， ，

（2）解：∵∠ACD＝90°，AC＝CD，

∴∠1＝∠D＝45°，

∵AE＝AC，

∴∠3＝∠5＝67.5°，

∴∠DEC＝180°－∠5＝112.5°

【解析】（1）根据同角的余角相等得出∠ 2 = ∠ 4 ， r然后利用AAS判断出ABC≌△DEC，再根据全等三角形的对应边相等得出结论；
（2）根据等腰直角三角形的性质知∠1＝∠D＝45°，又由知道顶角求等腰三角形底角的方法算出∠3＝∠5＝67.5°，利用邻补角的定义算出答案。
【考点精析】通过灵活运用等腰直角三角形和余角和补角的特征，掌握等腰直角三角形是两条直角边相等的直角三角形；等腰直角三角形的两个底角相等且等于45°；互余、互补是指两个角的数量关系，与两个角的位置无关即可以解答此题．