题目内容
【题目】如图,AD⊥BC,垂足为D.CD=1,AD=2,BD=4.
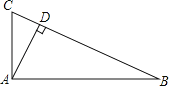
(1)求∠BAC的度数?并说明理由;
(2)P是边BC上一点,连结AP,当△ACP为等腰三角形时,求CP的长.
【答案】(1)∠BAC=90°;(2)CP的长为2或![]() 或2.5.
或2.5.
【解析】
试题分析:首先由勾股定理求出AC和AB,再由勾股定理逆定理证出△ABC为直角三角形得出∠BAC=90°;当△ACP为等腰三角形时,CP有三个解.
解:(1)∠BAC=90°;理由:
∵AD⊥BC,
∴∠ADC=∠ADB=90°;
由勾股定理可得 AC2=AD2+CD2=12+22=5,AB2=AD2+BD2=22+42=20;
∴AC2+AB2=25;
∵BC2=(BD+CD)2=52=25;
∴AC2+AB2=BC2;
∴△ABC是直角三角形;
∴∠BAC=90°;
(2)当△ACP为等腰三角形时,有三种情况:
①当AC=AP时,CP=2CD=2;
②当AC=CP时,∵AC=![]() ,∴CP=
,∴CP=![]() ;
;
③当CP=AP时,CP=![]() =2.5;
=2.5;
因此,当△ACP为等腰三角形时,CP的长为2或![]() 或2.5.
或2.5.

练习册系列答案
相关题目
【题目】某电信检修小组从A地出发,在东西向的公路上检修线路,如果规定向东行驶为正,向西行驶为负,一天中七次行驶纪录如下。(单位:km)
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 第七次 |
-3 | +7 | -9 | +8 | +6 | -5 | -4 |
(1)求收工时距A地多远?
(2)在第几次纪录时距A地最远?
(3)若每km耗油0.2升,问共耗油多少升?