题目内容
【题目】如图抛物线![]() 与
与![]() 轴交于A(1,0),
轴交于A(1,0),![]() 两点
两点

(1)求该抛物线的解析式;
(2)设(1)中的抛物线交![]() 轴于
轴于![]() 点,在该抛物线的对称轴上是否存在点
点,在该抛物线的对称轴上是否存在点![]() ,使得
,使得![]() 的周长最小?若存在,求出
的周长最小?若存在,求出![]() 点的坐标;若不存在,请说明理由。
点的坐标;若不存在,请说明理由。
【答案】(1)y=-x2-2x+3.(2)存在,(-1,2).
【解析】
试题分析:(1)将点A、点B的坐标代入可求出b、c的值,继而可得出该抛物线的解析式;
(2)连接BC,则BC与对称轴的交点,即是点M的位置,求出直线BC的解析式后,可得出点M的坐标.
试题解析:(1)把A(1,0)、B(-3,0)代入抛物线解析式可得:
![]() ,
,
解得:![]()
故抛物线的解析式为y=-x2-2x+3.
(2)存在.
由题意得,点B与点A关于抛物线的对称轴对称,连接BC,则BC与抛物线对称轴的交点是点M的位置,
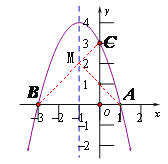
设直线BC解析式为y=kx+b,把B(-3,0)、C(0,3)代入得:
![]() ,
,
解得:![]() ,
,
则直线BC的解析式为y=x+3,
令MX=-1得My=2,
故点M的坐标为:(-1,2).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目