题目内容
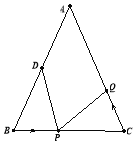
【题目】在![]() 中,AB= 20cm,BC=16cm,点D为线段AB的中点,动点P以2cm/s的速度从B点出发在射线BC上运动,同时点Q以a cm/s(a>0且a≠2)的速度从C点出发在线段CA上运动,设运动时间为x秒.
中,AB= 20cm,BC=16cm,点D为线段AB的中点,动点P以2cm/s的速度从B点出发在射线BC上运动,同时点Q以a cm/s(a>0且a≠2)的速度从C点出发在线段CA上运动,设运动时间为x秒.
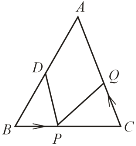
(1)若AB=AC,P在线段BC上,求当a为何值时,能够使△BPD和△CQP全等?
(2)若![]() ,求出发几秒后,
,求出发几秒后,![]() 为直角三角形?
为直角三角形?
(3)若![]() ,当
,当![]() 的度数为多少时,
的度数为多少时,![]() 为等腰三角形?(请直接写出答案,不必写出过程).
为等腰三角形?(请直接写出答案,不必写出过程).
【答案】(1)2.5cm/s;(2)2.5秒或10秒;(3)70°.
【解析】
试题分析:(1)根据等边对等角可得∠B=∠C,然后表示出BD、BP、PC、CQ,再根据全等三角形对应边相等,分①BD、PC是对应边,②BD与CQ是对应边两种情况讨论求解即可.(2)分类讨论①∠BDP和∠BPD两种情况讨论,然后根据直角三角形中30°角所对的直角边等于斜边的一半得出结论.
试题解析:(1)![]() ,
,![]() ,
, ![]() cm,D是AB的中点,
cm,D是AB的中点,![]() cm .
cm .![]() 点Q的速度与点P的速度不同,
点Q的速度与点P的速度不同,![]() ,要使△BPD和△CQP全等,则BP=CP=8cm,CQ=BD= 10cm ,
,要使△BPD和△CQP全等,则BP=CP=8cm,CQ=BD= 10cm , ![]() 秒 ,
秒 , ![]() cm/s .
cm/s .
(2)【1】当![]() 时,
时, ![]() ∴
∴ ![]() ,∴ 2 BP = BD = 10
,∴ 2 BP = BD = 10
∴ BP = 5 即2 x = 5 ∴x = 2.5.
【2】当![]() 时,
时,![]() ∴
∴ ![]() ,∴ BP = 2 BD = 20, 即2 x = 20 ∴x = 10
,∴ BP = 2 BD = 20, 即2 x = 20 ∴x = 10
![]() 当P出发2.5秒或10秒后,
当P出发2.5秒或10秒后,![]() 为直角三角形
为直角三角形
(3)![]() ,
,![]() ,
,![]() ,
,![]()

【题目】某商场在促销期间规定:商场内所有商品按标价的80%出售,同时当顾客在该商场消费满一定金额后,按如下方案获得相应金额的奖券:
消费金额a(元)范围 | 200≤a<400 | 400≤a<500 | 500≤a<700 | 700≤a<900 | … |
获得奖券的金额(元) | 30 | 60 | 100 | 130 | … |
根据上述促销方法,顾客在商场内购物可以获得双重优惠。例如,购买标价为450元的商品,则消费金额为![]() 元,获得的优惠额为450×(1-80%)+30=120元,设购买该商品得到的优惠率=购买商品获得的优惠额÷商品的标价。
元,获得的优惠额为450×(1-80%)+30=120元,设购买该商品得到的优惠率=购买商品获得的优惠额÷商品的标价。
(1)购买一件标价为1000元的商品,顾客得到的优惠率是多少?
(2)对于标价在500元与800元之间(含500元和800元)的商品,顾客购买标价为多少元的商品,可以得到![]() 的优惠率?
的优惠率?