题目内容
【题目】在△ABC中,BC边上的高AG平分∠BAC.
(1)如图1,求证:AB=AC.
(2)如图2,点D、E在△ABC的边BC上,AD=AE,BC=10cm,DE=6cm,求BD的长.

【答案】(1)证明见解析;(2)2cm
【解析】
(1)想办法证明∠B=∠C即可解决问题.
(2)如图2中,作AG⊥BC于G.利用等腰三角形的三线合一的性质证明BD=CE即可解决问题.
(1)证明:如图1中,
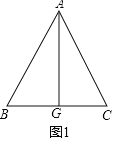
∵AG为∠BAC的平分线,
∴∠BAG=∠CAG,
∵AG为BC边上高
∴∠AGB=∠AGC=90°,
∴根据三角形内角和定理可知:∠B=∠C,
∴AB=AC.
(2)如图2中,作AG⊥BC于G.
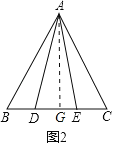
∵AB=AC,AG⊥BC,
∴BG=CG,
∵AD=AE,AG⊥BC,
∴DG=EG,
∴BG﹣DG=CG﹣EG,
∴BD=CE,
∵BC=10cm,DE=6cm,
∴BD=2cm.

练习册系列答案
相关题目








