Question

【题目】已知等腰直角△ABC，∠ABC＝90°，AB＝BC＝4，平面内有一点D，连接CD、AD，若CD＝2，AD＝6，则∠BCD＝_____.

Answer 1

【答案】135°或45°

【解析】

根据勾股定理的逆定理证明△ACD为直角三角形，求出∠ACD＝90°，再求出∠ACB＝45°问题即可解决.

解：∵∠ABC＝90°，AB＝BC＝4，

∴AC2＝42+42＝32，而CD2＝4，AD2＝62＝36，

∴AD2＝AC2+CD2，

∴△ACD为直角三角形，∠ACD＝90°；

∵△ABC为等腰直角三角形，

∴∠ACB＝45°，

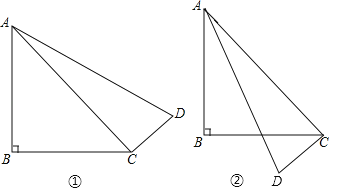
∴如图①：∠BCD＝90°+45°＝135°；

如图②：∠BCD＝90°﹣45°＝45°.

故∠BCD＝135°或45°.

故答案为：135°或45°.