题目内容
【题目】在探索三角形全等的条件时，老师给出了定长线段a，b，且长度为b的边所对的角为n°(0＜n＜90°)小明和小亮按照所给条件分别画出了图1中的三角形，他们把两个三角形重合在一起(如图2)，其中AB＝a，BD＝BC＝b，发现它们不全等，但他们对该图形产生了浓厚兴趣，并进行了进一步的探究：
(1)当n＝45时(如图2)，小明测得∠ABC＝65°，请根据小明的测量结果，求∠ABD的大小；
(2)当n≠45时，将△ABD沿AB翻折，得到△ABD′(如图3)，小明和小亮发现∠D′BC的大小与角度n有关，请找出它们的关系，并说明理由；
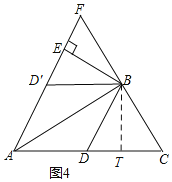
(3)如图4，在(2)问的基础上，过点B作AD′的垂线，垂足为点E，延长AE到点F，使得EF＝
(AD+AC)，连接BF，请判断△ABF的形状，并说明理由.
【答案】(1)25°；(2)∠D'BC=180°﹣2n°，证明见解析；(3)等腰三角形，证明见解析.
【解析】
(1)先根据三角形的内角和得∠C＝70°，由等腰三角形的性质得∠BDC＝70°，从而得∠CBD的度数，可得结论；(2)设∠BDC＝∠C＝α，根据三角形的内角和与三角形外角的性质分别表示∠ABD和∠DBC，相加可得结论；(3)作垂线BT，根据角平分线的性质得：BE＝BT，证明Rt△ABE≌Rt△ABT(HL)，得AE＝AT，证明BE是AF的垂直平分线，可得结论.
解：(1)如图2，△ABC中，∠A＝n°＝45°，∠ABC＝65°，
∴∠C＝180°﹣45°﹣65°＝70°，
∵BD＝BC，
∴∠BDC＝∠C＝70°，
∴∠DBC＝180°﹣2×70°＝40°，
∴∠ABD＝65°﹣40°＝25°；
(2)如图3，∠D'BC＝180°﹣2n°，理由是：
设∠BDC＝∠C＝α，
∴∠DBC＝180°﹣2α，
△ADB中，∠BDC＝∠DAB+∠ABD，
即α＝n°+∠ABD，
∴∠ABD＝α﹣n°，
由翻折得：∠ABD'＝∠ABD＝α﹣n°，
∴∠D'BC＝∠D'BD+∠DBC＝2∠ABD+∠DBC＝2(α﹣n°)+(180°﹣2α)＝180°﹣2n°；
(3)△ABF是等腰三角形，且BF＝AB，理由是：
如图4，过B作BT⊥AC于T，
由折叠得：∠D'BC＝∠DAB，
∵BE⊥AF，
∴BE＝BT，
在Rt△ABE和Rt△ABT中，
，
∴Rt△ABE≌Rt△ABT(HL)，
∴AE＝AT，
∵AD＝AD'，
∴DT＝D'E＝TC，
∴
＝AT，
∵EF＝，
∴AT＝EF＝AE，
∵BE⊥AF，即BE是AF的垂直平分线，
∴BF＝AB，
∴△ABF是等腰三角形.
