Question

【题目】如图，Rt△ABC中，∠ACB＝90°，AC＝BC，点D在斜边AB上，且AD＝AC，过点B作BE⊥CD，交直线CD于点E.

(1)求∠BCD的度数；

(2)作AF⊥CD于点F，求证：△AFD≌△CEB；

(3)请直接写出CD与BE的数量关系(不需要证明)．

Answer 1

【答案】(1) ∠BCD＝＝22.5°；(2)见解析 (3) CD＝2BE.

【解析】

（1）根据等腰直角三角形的性质得到∠CAB＝∠CBA＝45°，根据等腰三角形的性质计算即可；（2）根据全等三角形的判定证明△AFD≌△CEB即可．（3）根据全等三角形的性质证明即可．

解：(1)∵∠ACB＝90°，AC＝BC，

∴∠CAB＝∠CBA＝45°.

∵AD＝AC，

∴∠ACD＝∠ADC＝ ＝67.5°.

∴∠BCD＝90°－67.5°＝22.5°.

(2)证明：∵AD＝AC，AF⊥CD，

∴CF＝FD＝CD，∠FAD＝∠CAB＝22.5°.

又∵AC＝CB，∴AD＝CB，

在△AFD和△CEB中，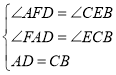

∴△AFD≌△CEB(AAS)．

(3)∵△AFD≌△CEB，

∴BE=DF，

又∵AD＝AC，且AF⊥CD

∴CD=2DF,

∴CD＝2BE.