题目内容
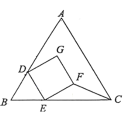
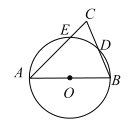
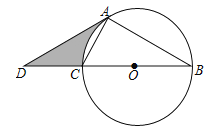
【题目】如图,以![]() 的边BC为直径作⊙O,点A在⊙O上,点D在线段BC的延长线上,AD=AB,
的边BC为直径作⊙O,点A在⊙O上,点D在线段BC的延长线上,AD=AB,![]() ,若
,若![]() 的长为
的长为![]() ,则图中阴影部分的面积__________.
,则图中阴影部分的面积__________.
【答案】![]()
【解析】
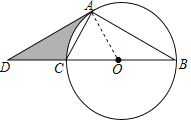
连接OA,如图,则∠COA=2∠B,由AD=AB可得∠B=∠D,进而可利用三角形的内角和得出∠OAD=90°,由弧长公式可求出半径OA的长,从而可在Rt△OAD中,利用解直角三角形的知识求出AD的长,然后根据S阴影=S△OAD﹣S扇形COA计算即可.
解:连接OA,如图,则∠COA=2∠B,
∵AD=AB,∴∠B=∠D=30°,
∴∠COA=60°,
∴∠OAD=180°﹣60°﹣30°=90°,
∵![]() 的长为
的长为![]() ,
,
∴![]() ,∴OA=2,
,∴OA=2,
在Rt△OAD中,OA=2,∠D=30°,
∴OD=2OA=4,AD=2![]() ,
,
∴S△OAD=![]() OAAD=
OAAD=![]() ×2×2
×2×2![]() =2
=2![]() ,
,
∵∠COA=60°,
∴S扇形COA=![]() ,
,
所以S阴影=S△OAD﹣S扇形COA=![]() .
.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目