题目内容
【题目】如图,A,B是反比例函数y=![]() 在第一象限内的图象上的两点,且A,B两点的横坐标分别是2和4,则△OAB的面积是( )
在第一象限内的图象上的两点,且A,B两点的横坐标分别是2和4,则△OAB的面积是( )
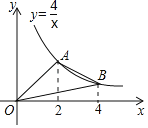
A. 4 B. 3 C. 2 D. 1
【答案】B
【解析】先根据反比例函数图象上点的坐标特征及A,B两点的横坐标,求出A(2,2),B(4,1).再过A,B两点分别作AC⊥x轴于C,BD⊥x轴于D,根据反比例函数系数k的几何意义得出S△AOC=S△BOD=![]() ×4=2.根据S四边形AODB=S△AOB+S△BOD=S△AOC+S梯形ABDC,得出S△AOB=S梯形ABDC,利用梯形面积公式求出S梯形ABDC=
×4=2.根据S四边形AODB=S△AOB+S△BOD=S△AOC+S梯形ABDC,得出S△AOB=S梯形ABDC,利用梯形面积公式求出S梯形ABDC=![]() (BD+AC)CD=
(BD+AC)CD=![]() ×(1+2)×2=3,从而得出S△AOB=3.
×(1+2)×2=3,从而得出S△AOB=3.
∵A,B是反比例函数y=![]() 在第一象限内的图象上的两点,
在第一象限内的图象上的两点,
且A,B两点的横坐标分别是2和4,
∴当x=2时,y=2,即A(2,2),
当x=4时,y=1,即B(4,1),
如图,过A,B两点分别作AC⊥x轴于C,BD⊥x轴于D,
则S△AOC=S△BOD=![]() ×4=2,
×4=2,
∵S四边形AODB=S△AOB+S△BOD=S△AOC+S梯形ABDC,
∴S△AOB=S梯形ABDC,
∵S梯形ABDC=![]() (BD+AC)CD=
(BD+AC)CD=![]() ×(1+2)×2=3,
×(1+2)×2=3,
∴S△AOB=3,
故选B.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
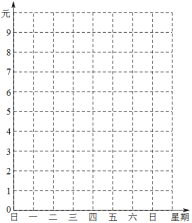
【题目】小张上星期六买进某公司的股票2000股,每股30元,下表是本周内每日该股票的涨跌情况(单位:元):
星期 | 一 | 二 | 三 | 四 | 五 | 六 |
每股涨跌 |
|
|
|
|
|
|
(1)星期三收盘时,每股是多少元?
(2)本周内最高价是每股多少元?
(3)请用拆线统计图表示该股票这六天的涨跌情况.(请在已设计好的坐标纸里画图)
(4)已知小张买过股票时付了1.5‰的手续费,卖出时需付成交额1.5‰的手续费和1‰的交易税,如小张在星期六收盘时将股票全部卖出,它的收益情况如何?