题目内容
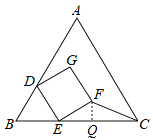
【题目】如图,等边三角形ABC和正方形DEFG按如图所示摆放,其中 D,E两点分别在AB,BC上,且BD=DE.若AB=12,DE=4,则△EFC的面积为( )
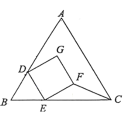
A.4B.8C.12D.16
【答案】B
【解析】
过F作FQ⊥BC于Q,根据等边三角形的性质和判定和正方形的性质求出BE=2,∠BED=60°,∠DEF=90°,EF=4,求出∠FEQ,求出CE和FQ,即可求出答案.
过F作FQ⊥BC于Q,则∠FQE=90°,
∵△ABC是等边三角形,AB=12,
∴BC=AB=12,∠B=60°,
∵BD=BE,DE=4,
∴△BED是等边三角形,且边长为4,
∴BE=DE=4,∠BED=60°,
∴CE=BC-BE=8,
∵四边形DEFG是正方形,DE=4,
∴EF=DE=4,∠DEF=90°,
∴∠FEC=180°-60°-90°=30°,
∴QF=![]() EF=2,
EF=2,
∴△EFC的面积为![]() ×CE×FQ=
×CE×FQ=![]() ×8×2=8,
×8×2=8,
故选:B.

练习册系列答案
相关题目