题目内容
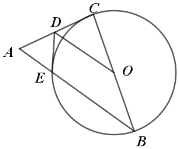
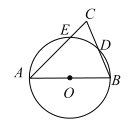
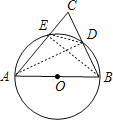
【题目】如图,AB为![]() 的直径,AC,BC分别交
的直径,AC,BC分别交![]() 于点E,D,
于点E,D,![]() ,
,![]() .现给出以下四个结论:①
.现给出以下四个结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中正确结论的序号是________.(填写所有正确结论的序号)
.其中正确结论的序号是________.(填写所有正确结论的序号)
【答案】②④
【解析】
连结AD、BE,DE,如图,根据圆周角定理得∠ADB=90°,则AD⊥BC,加上CD=BD,根据等腰三角形的判定即可得到AB=AC;再根据等腰三角形的性质和三角形内角和定理可计算出∠BAC=40°;由AB为直径得到∠AEB=90°,则∠ABE=50°,根据圆周角定理可判断![]() ;接着证明△CED∽△CBA,利用相似比得到CECA=CDCB,然后利用等线段代换即可得到CECA=2BD2.
;接着证明△CED∽△CBA,利用相似比得到CECA=CDCB,然后利用等线段代换即可得到CECA=2BD2.
解:连结AD、BE,DE,如图,
∵AB为直径,
∴∠ADB=90°,
∴AD⊥BC,
而CD=BD,
∴AB=AC,所以②正确;
∵∠C=70°,
∴∠ABC=∠C=70°,
∴∠BAC=40°,所以①错误;
∵AB为直径,
∴∠AEB=90°,
∴∠ABE=50°,
∴![]() ,所以③错误;
,所以③错误;
∵∠CED=∠CBA,
而∠C公共,
∴△CED∽△CBA,
∴![]() ,
,
∴CECA=CDCB,
∴CECA=BD2BD=2BD2,所以④正确.
故答案为②④.

练习册系列答案
相关题目