题目内容
【题目】某服装厂承揽一项生产夏凉小衫1600件的任务，计划用t天完成．
（1）写出每天生产夏凉小衫w（件）与生产时间t（天）（t＞4）之间的函数关系式;
（2）由于气温提前升高，商家与服装厂商议调整计划，决定提前4天交货，那么服装厂每天要多做多少件夏凉小衫才能完成任务？
【答案】（1）
；（2）
【解析】试题分析：（1）根据实际意义可列出夏凉小衫w（件）与生产时间t（天）（t＞4）之间的函数关系式；
（2）根据题意列出t﹣4对应的式子
，与（1）中的式子相减即可．
试题解析：（1）由题意可得，函数关系式为：w=
（
）；
（2）
=
=
．（或
）．
答：每天多做（或）件夏凉小衫才能完成任务．
考点：反比例函数的应用．
【题型】解答题
【结束】
13
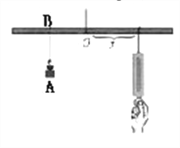
【题目】如图所示，小华设计了一个探究杠杆平衡条件的实验：在一根匀质的木杆中点O左侧固定位置B处悬挂重物A，在中点O右侧用一个弹簧秤向下拉，改变弹簧秤与点O的距离x（cm），观察弹簧秤的示数y（N）的变化情况。实验数据记录如下：
x（cm） | … | 10 | 15 | 20 | 25 | 30 | … |
y（N） | … | 30 | 20 | 15 | 12 | 10 | … |
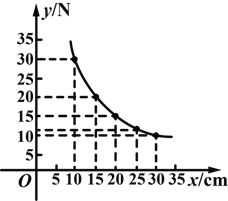
（1）把上表中x，y的各组对应值作为点的坐标，在坐标系中描出相应的点，用平滑曲线连接这些点并观察所得的图象，猜测y（N）与x（cm）之间的函数关系，并求出函数关系式；
（2）当弹簧秤的示数为24N时，弹簧秤与O点的距离是多少cm？
随着弹簧秤与O点的距离不断减小，弹簧秤上的示数将发生怎样的变化？
【答案】（1）图象见解析；
；（2）随着弹簧秤与0点的距离不断减小，弹簧秤上的示数不断增大.
【解析】(1)取实验数据(10，30)，(15，20)，(20，15)，(25，12)，(30，10)，并在平面直角坐标系中描出相应的点，用平滑的曲线连接这些点，得到如图所示的图象．由图象猜测y与x之间的函数关系为反比例函数关系．
设反比例函数为
(k≠0)，把x＝10，y＝30代入，
得k＝300，
∴，将各点代入均适合．
∴y与x之间的函数解析式为．
(2)把y＝24代入，得x＝12.5．
∴当弹簧秤的示数为24N时，弹簧秤与O点之间的距离是12.5cm．
随着弹簧秤与O点之间的距离不断减小，弹簧秤的示教不断增大．
