题目内容
【题目】（10分）直线y=x﹣6与x轴、y轴分别交于点A、B，点E从B点，出发以每秒1个单位的速度沿线段BO向O点移动（与B、O点不重合），过E作EF∥AB，交x轴于F．将四边形ABEF沿EF折叠，得到四边形DCEF，设点E的运动时间为t秒．
（1）①直线y=x﹣6与坐标轴交点坐标是A（ ， ），B（ ， ）；
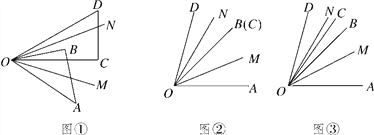
②画出t=2时，四边形ABEF沿EF折叠后的图形（不写画法）；
（2）若CD交y轴于H点，求证：四边形DHEF为平行四边形；并求t为何值时，四边形DHEF为菱形（计算结果不需化简）；
【答案】（1）①A（6，0），B（0，﹣6）；②见解析；（2）t=12﹣6
【解析】整体分析：
（1）①分别把x=0，y=0代入方程y=x﹣6，可得A，B的坐标；②先确定点E，F的坐标，再根据轴对称的性质，确定点A，B关于EF的对称点D，C的坐标；（2）用两组对边分别平行的四边形是平行四边形证明四边形DHEF为平行四边形，由DF=EF列方程求解.
解：（1）①当y=0，x﹣6=0，解得x=6；
当x=0时，y=-6.
所以直线y=x﹣6与坐标轴交点坐标是：A（6，0），B（0，﹣6）；
②如图1，四边形DCEF即为四边形ABEF沿EF折叠后的图形；
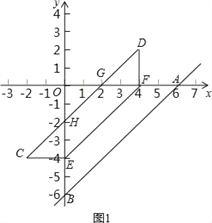
（2）∵四边形DCEF与四边形ABEF关于直线EF对称，
又AB∥EF，∴CD∥EF．
∵OA=OB，∠AOB=90°，∴∠BAO=45°．
∵AB∥EF，∴∠AFE=135°，∴∠DFE=∠AFE=135°．
∴∠AFD=360°﹣2×135°=90°，即DF⊥x轴．
∴DF∥EH，
∴四边形DHEF为平行四边形．
要使四边形DHEF为菱形，
只需EF=DF，
∵AB∥EF，∠FAB=∠EBA，∴FA=EB．
∴DF=FA=EB=t．
又∵OE=OF=6﹣t，∴EF=
（6-t）．
∴
（6-t）=t．
∴t=
=12﹣
．
∴当t=12﹣
时，四边形DHEF为菱形．
【题目】某服装厂承揽一项生产夏凉小衫1600件的任务，计划用t天完成．
（1）写出每天生产夏凉小衫w（件）与生产时间t（天）（t＞4）之间的函数关系式;
（2）由于气温提前升高，商家与服装厂商议调整计划，决定提前4天交货，那么服装厂每天要多做多少件夏凉小衫才能完成任务？
【答案】（1）
；（2）
【解析】试题分析：（1）根据实际意义可列出夏凉小衫w（件）与生产时间t（天）（t＞4）之间的函数关系式；
（2）根据题意列出t﹣4对应的式子
，与（1）中的式子相减即可．
试题解析：（1）由题意可得，函数关系式为：w=
（
）；
（2）
=
=
．（或
）．
答：每天多做（或）件夏凉小衫才能完成任务．
考点：反比例函数的应用．
【题型】解答题
【结束】
13
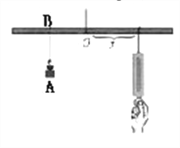
【题目】如图所示，小华设计了一个探究杠杆平衡条件的实验：在一根匀质的木杆中点O左侧固定位置B处悬挂重物A，在中点O右侧用一个弹簧秤向下拉，改变弹簧秤与点O的距离x（cm），观察弹簧秤的示数y（N）的变化情况。实验数据记录如下：
x（cm） | … | 10 | 15 | 20 | 25 | 30 | … |
y（N） | … | 30 | 20 | 15 | 12 | 10 | … |
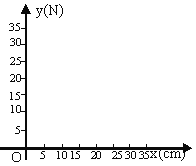
（1）把上表中x，y的各组对应值作为点的坐标，在坐标系中描出相应的点，用平滑曲线连接这些点并观察所得的图象，猜测y（N）与x（cm）之间的函数关系，并求出函数关系式；
（2）当弹簧秤的示数为24N时，弹簧秤与O点的距离是多少cm？
随着弹簧秤与O点的距离不断减小，弹簧秤上的示数将发生怎样的变化？
