题目内容
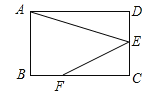
【题目】如图,在坡角为30°的山坡上有一铁塔AB,其正前方矗立着一大型广告牌,当阳光与水平线成45°角时,测得铁塔AB落在斜坡上的影子BD的长为6米,落在广告牌上的影子CD的长为4米,求铁塔AB的高(AB,CD均与水平面垂直,结果保留根号).
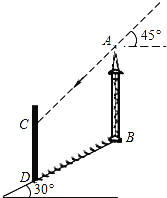
【答案】铁塔AB的高为(3![]() +1)m.
+1)m.
【解析】试题过点C作CE⊥AB于E,过点B作BF⊥CD于F,过点B作BF⊥CD于F,在在Rt△BFD中,分别求出![]() 的长度, 然后根据矩形
的长度, 然后根据矩形![]() 的性质得到:
的性质得到: ![]() 然后通过解Rt△ACE求得
然后通过解Rt△ACE求得![]() 结合图形来求得
结合图形来求得![]() 的长度.
的长度.
试题解析:
过点C作CE⊥AB于E,过点B作BF⊥CD于F,过点B作BF⊥CD于F,
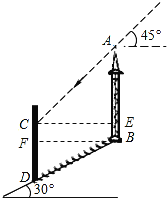
在Rt△BFD中,
![]()
∵BD=6,
![]()
∵AB∥CD,CE⊥AB,BF⊥CD,
∴四边形BFCE为矩形,
![]() .则CF=BE=CDDF=1,
.则CF=BE=CDDF=1,
在Rt△ACE中, ![]()
![]()
![]()
即:铁塔AB的高为![]() 米.
米.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目