Question

【题目】已知O为坐标原点，A，B分别在y轴、x轴正半轴上，D是x轴正半轴上一动点，AD＝DE，∠ADE＝α，矩形AOBC的面积为32且AC＝2BC．

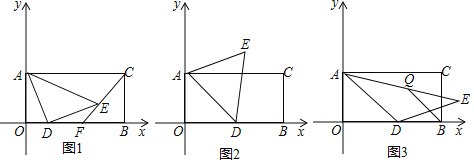
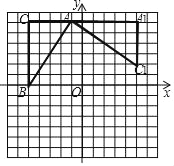
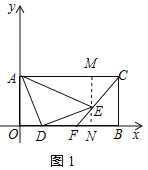
（1）如图1，当α＝90°时，直线CE交x轴于点F，求证：F为OB中点；

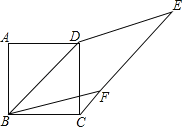
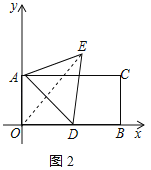
（2）如图2，当α＝60°时，若D是OB中点，求E点坐标；

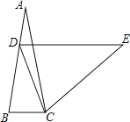
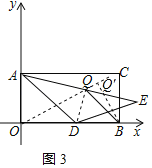
（3）如图3，当α＝120°时，Q是AE的中点，求D点运动过程中BQ的最小值．

Answer 1

【答案】（1）见解析；（2）（2+2，2+2）；（3）4

【解析】

（1）由题意得出BC＝4，AC＝8，过点E作MN⊥AC交AC于点M、交OB于点N，则四边形AONM为矩形、四边形MNBC为矩形，证明△END≌△DOA（AAS），得出OA＝DN＝4，EN＝OD，设OD＝EN＝x，则ME＝MN﹣EN＝4﹣x，MC＝AC﹣AM＝AC﹣ON＝AC﹣OD﹣DN＝8﹣x﹣4＝4﹣x，证明△CME是等腰直角三角形，得出∠MCE＝45°，证出△CBF是等腰直角三角形，得出BC＝BF＝4，证出OF＝BF即可；

（2）证明△AOD是等腰直角三角形，得出AD＝4，连接OE，证明△ADE为等边三角形，得出EA＝ED，证明OE垂直平分AD，由等腰三角形的性质得出∠AOE＝∠DOE＝45°，由勾股定理得出OE＝2（+），即可得出答案；

（3）连接DQ、OQ，由等腰三角形的性质得出DQ⊥AE，证明A、O、D、Q四点共圆，由等腰三角形的性质得出∠DAQ＝30°，由圆周角定理得出∠QOD＝30°，得出Q点的运动轨迹为与x轴的一个夹角为30°的射线，当BQ⊥MN时，BQ有最小值，由含30°角的直角三角形的性质即可得出答案．

（1）证明：∵矩形AOBC的面积为32且AC＝2BC，

∴S矩形AOBC＝ACBC＝2BCBC＝2BC2＝32，

∴BC＝4，

∴AC＝8，

过点E作MN⊥AC交AC于点M、交OB于点N，如图1所示：

则四边形AONM为矩形、四边形MNBC为矩形，

∴OA＝MN＝BC＝4，AM+CM＝ON+BN＝AC＝OB＝8，∠END＝∠DOA＝90°，

∵∠ADE＝90°，

∴∠ADO+∠EDN＝90°，

∵∠ADO+∠DAO＝90°，

∴∠EDN＝∠DAO，

在△END和△DOA中，

，

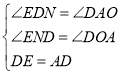∴△END≌△DOA（AAS），

∴OA＝DN＝4，EN＝OD，

设OD＝EN＝x，

则ME＝MN﹣EN＝4﹣x，MC＝AC﹣AM＝AC﹣ON＝AC﹣OD﹣DN＝8﹣x﹣4＝4﹣x，

∴ME＝MC，

∴△CME是等腰直角三角形，

∴∠MCE＝45°，

∴∠FCB＝45°，

∴△CBF是等腰直角三角形，

∴BC＝BF＝4，

∴OF＝OB﹣F＝8﹣4＝4，

∴OF＝BF，

∴F为OB中点；

（2）解：∵D是OB中点，

∴OB＝2OA＝2OD＝8，

∴OA＝OD＝4，

∴△AOD是等腰直角三角形，

∴AD＝4，

连接OE，如图2所示：

∵AD＝DE，∠ADE＝60°

∴△ADE为等边三角形，

∴EA＝ED，

∵AO＝DO，

∴OE垂直平分AD，

∴∠AOE＝∠DOE＝45°，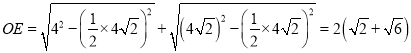

∴E点的横纵坐标为都为：×2（+）＝2+2，

∴E点坐标为（2+2，2+2），

（3）解：连接DQ、OQ，如图3所示：

∵AD＝DE，Q是AE的中点，

∴DQ⊥AE，

∵AO⊥OD，

∴∠AOD+∠AOD＝180°，

∴A、O、D、Q四点共圆，

∵∠ADE＝120°，AD＝DE，

∴∠DAQ＝∠DEA＝30°，

∴∠QOD＝∠DAQ＝30°，

∴Q点的运动轨迹为与x轴的一个夹角为30°的射线，

∴当BQ⊥MN时，BQ有最小值，

BQ＝OB＝×8＝4．