题目内容
【题目】为庆祝中华人民共和国七十周年华诞,某校举行书画大赛,准备购买甲、乙两种文具,奖励在活动中表现优秀的师生已知用300元购买甲种文具的个数是用50元购买乙种文具个数的2倍,购买1个甲种文具比购买1个乙种文具多花费10元.
(1)求购买一个甲种文具、一个乙种文具各需多少元;
(2)若学校计划购买这两种文具共120个,投入资金不多于1000元,且甲种文具至少购买36个,求有多少种购买方案.
【答案】(1)购买一个甲种文具15元,一个乙种文具5元;(2)有5种购买方案
【解析】
(1)设购买一个乙种文具x元,则一个甲种文具(x+10)元,根据“用300元购买甲种文具的个数是用50元购买乙种文具个数的2倍,”列方程解答即可;
(2)设购买甲种文具a个,则购买乙种文具(120-a)个,根据题意列不等式组,解之即可得出a的取值范围,结合a为正整数即可得出a的值,进而可找出各购买方案.
解:(1)设购买一个乙种文具x元,则一个甲种文具(x+10)元,由题意得:![]() ,解得x=5,
,解得x=5,
经检验,x=5是原方程的解,且符合题意,
x+10=15(元),
答:购买一个甲种文具15元,一个乙种文具5元;
(2)设购买甲种文具a个,则购买乙种文具(120-a)个,根据题意得: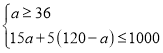 ,
,
解得36≤a≤40,
∵a是正整数,
∴a=36,37,38,39,40.
∴有5种购买方案.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
【题目】某体育运动学校准备在甲、已两位射箭选手中选出成绩比较稳定的一人参加集训,两人各射击了5箭,已知他们的总成绩(单位:环)相同,如下表所示:
第1次 | 第2次 | 第3次 | 第4次 | 第5次 | |
甲成绩 | 9 | 4 | 7 | 4 | 6 |
乙成绩 | 7 | 5 | 7 | a | 7 |
(1)试求出表中a的值;
(2)请你通过计算,从平均数和方差的角度分析,谁将被选中.
[注:平均数x=![]() ;方差
;方差![]() ].
].