题目内容
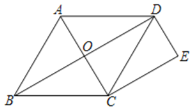
【题目】凸四边形ABCD的两条对角线和两条边的长度都为1,则四边形ABCD中最大内角度数为( )
A.150°B.135°C.120°D.105°
【答案】A
【解析】
首先,这两条相等的边不可能是对边,如果两条对边相等,则对角线至少有一条大于这两条边.也就是说这两条相等的边是邻边(设为AB、AC),加上连接这两条边的那条对角线(BC),就是一个等边三角形(ABC);当另一条对角线(AD)垂直于对角线(BC)时,∠BDC是最大内角150°;当AD不垂直于BC时,∠BDC介于150°到90°之间,而∠ABD和∠ACD都介于75°到150°之间.所以最大的内角是150°.
解:如图:

∵AB=AC=BC,
∴△ABC是等边三角形,
当另一条对角线AD⊥BC时,∠BDC=150°;
当AD不垂直于BC时,∠BDC介于150°到90°之间,而∠ABD和∠ACD都介于75°到150°之间.
所以最大的内角是150°.
故选:A.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目