Question

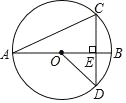
【题目】如图，线段 AB 是⊙O 的直径，弦 CD⊥AB，AB=8，∠CAB=22.5°，则 CD的长等于___________________________．

Answer 1

【答案】4

【解析】

连接 OC，如图所示，由直径 AB 垂直于 CD，利用垂径定理得到 E 为CD 的中点，即 CE=DE，由 OA=OC，利用等边对等角得到一对角相等，确定出三角形 COE 为等腰直角三角形，求出 CE 的长，进而得出 CD．

连接 OC，如图所示：

∵AB 是⊙O 的直径，弦 CD⊥AB，

∴OC= AB=4，

∵OA=OC，

∴∠A=∠OCA=22.5°，

∵∠COE 为△AOC 的外角，

∴∠COE=45°，

∴△COE 为等腰直角三角形，

∴CE= OC=，

∴CD=2CE=，

故答案为：.