题目内容
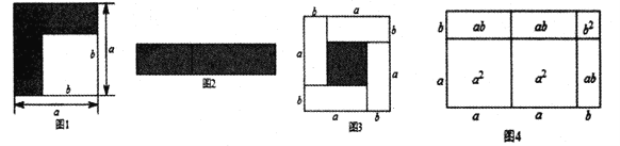
【题目】如图,AB为⊙O的直径,弦CD垂直平分OB于点E,点F在AB延长线上,∠AFC=30°.
(1)求证:CF为⊙O的切线.
(2)若半径ON⊥AD于点M,CE=![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.
【答案】(1)证明见解析;(2)![]() .
.
【解析】试题分析: (1)由CD垂直平分OB,得到E为OB的中点,且CD与OB垂直,又OB=OC,可得OE等于OC的一半,在直角三角形OEC中,根据锐角三角函数的定义,得到sin∠ECO的值为![]() ,可得∠ECO为30°,进而得到∠EOC为60°,又∠CFO为30°,可得∠OCF为直角,由OC为圆O的半径,可得CF为圆的切线,
,可得∠ECO为30°,进而得到∠EOC为60°,又∠CFO为30°,可得∠OCF为直角,由OC为圆O的半径,可得CF为圆的切线,
(2)由(1)得出的∠COF=60°,根据对称性可得∠EOD为60°,进而得到∠DOA=120°,由OA=OD,且OM与AD垂直,根据“三线合一”得到∠DOM为60°,在直角三角形OCE中,由CE的长及∠ECO=30°,可求出半径OC的长,又在直角三角形OMD中,由∠MDO=30°,半径OD=2,可求出MD及OM的长,然后利用扇形ODN的面积减去三角形ODM的面积即可求出阴影部分的面积.
试题解析:(1)证明:∵CD垂直平分OB,
∴OE=![]() OB,∠CEO=90°,
OB,∠CEO=90°,
∵OB=OC,
∴OE=![]() OC,
OC,
在Rt△COE中,sin∠ECO=![]() =
=![]() ,
,
∴∠ECO=30°,
∴∠EOC=60°,
∵∠CFO=30°,
∴∠OCF=90°,又OC是⊙O的半径,
∴CF是⊙O的切线,
(2)解:由(1)可得∠COF=60°,
由圆的轴对称性可得∠EOD=60°,∴∠DOA=120°,
∵OM⊥AD,OA=OD,∴∠DOM=60°,
在Rt△COE中,CE=![]() ,∠ECO=30°,cos∠ECO=
,∠ECO=30°,cos∠ECO=![]() ,
,
∴OC=2,
在Rt△ODM中,OD=2,∠ADO=30°,
∴OM=ODsin30°=1,MD=ODcos30°=![]() ,
,
∴S扇形OND=![]() ,
,
∴S△OMD=![]() OMDM=
OMDM=![]() ,
,
∴S阴影=S扇形OND﹣S△OMD=![]() .
.

【题目】如图,点B、E分别在AC、DF上,AF分别交BD、CE于点M、N,∠A=∠F,∠1=∠2.
(1)求证:四边形BCED是平行四边形;
(2)已知DE=2,连接BN,若BN平分∠DBC,求CN的长.

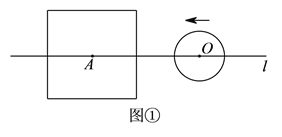
【题目】设边长为![]() 的正方形的中心
的正方形的中心![]() 在直线
在直线![]() 上,它的一组对边垂直于直线
上,它的一组对边垂直于直线![]() ,半径为
,半径为![]() 的圆的圆心
的圆的圆心![]() 在直线
在直线![]() 上运动,
上运动,![]() 、
、![]() 两点之间的距离为
两点之间的距离为![]() .
.
(![]() )如图①,当
)如图①,当![]() 时,填表:
时,填表:
| ⊙ |
|
|
|
|
| __________ |
| __________ |
| __________ |
(![]() )如图②,⊙
)如图②,⊙![]() 与正方形有
与正方形有![]() 个公共点
个公共点![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,求此时
,求此时![]() 与
与![]() 之间的数量关系:
之间的数量关系:

(![]() )由(
)由(![]() )可知,
)可知,![]() 、
、![]() 、
、![]() 之间的数量关系和⊙
之间的数量关系和⊙![]() 与正方形的公共点个数密切相关.当
与正方形的公共点个数密切相关.当![]() 时,请根据
时,请根据![]() 、
、![]() 、
、![]() 之间的数量关系,判断⊙
之间的数量关系,判断⊙![]() 与正方形的公共点个数.
与正方形的公共点个数.
(![]() )当
)当![]() 与
与![]() 之间满足(
之间满足(![]() )中的数量关系时,⊙
)中的数量关系时,⊙![]() 与正方形的公共点个数为__________.
与正方形的公共点个数为__________.