题目内容
【题目】已知点A(a,3),点C(5,c),点B的纵坐标为6且横纵坐标互为相反数,直线AC![]() 轴,直线CB
轴,直线CB![]() 轴:
轴:
(1)写出A、B、C三点坐标;
(2)求△ABC的面积;
(3)若P为线段OB上动点且点P的横、纵坐标互为相反数,当△BCP的面积大于12小于16时,求点P横坐标取值范围.

【答案】(1)A(5,3),B(-6,6),C(5,6);(2)![]() ;(3)点P横坐标取值范围为:-
;(3)点P横坐标取值范围为:-![]() <a<-
<a<-![]() .
.
【解析】
(1)根据题意得出A和C的横坐标相同,B和C的纵坐标相同,得出A(5,3),C(5,6),由角平分线的性质得出B的坐标;
(2)求出BC=5-(-6)=11,即可得出△ABC的面积;
(3)设P的坐标为(a,-a),则△BCP的面积=![]() ×11×(6+a),根据题意得出不等式12<
×11×(6+a),根据题意得出不等式12<![]() ×11×(6+a)<16,解不等式即可.
×11×(6+a)<16,解不等式即可.
解:(1)如图所示:
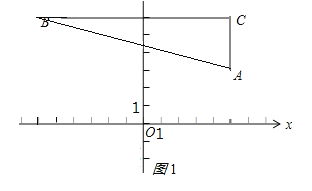
∵AC⊥x轴,CB⊥y轴,
∴A和C的横坐标相同,B和C的纵坐标相同,
∴A(5,3),C(5,6),
∵点B的纵坐标为6且横纵坐标互为相反数,
∴B(-6,6);
(2)∵BC=5-(-6)=11,
∴△ABC的面积=![]() ×11×(6-3)=
×11×(6-3)=![]() ;
;
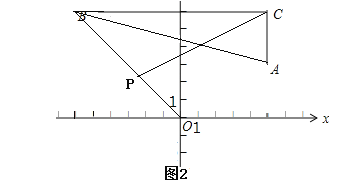
(3)设P的坐标为(a,-a),
则△BCP的面积=![]() ×11×(6+a),
×11×(6+a),
∵△BCP面积大于12小于16,
∴12<![]() ×11×(6+a)<16,
×11×(6+a)<16,
解得:-![]() <a<-
<a<-![]() ;
;
即点P横坐标取值范围为:-![]() <a<-
<a<-![]() .
.
故答案为:(1)A(5,3),B(-6,6),C(5,6);(2)![]() ;(3)点P横坐标取值范围为:-
;(3)点P横坐标取值范围为:-![]() <a<-
<a<-![]() .
.

练习册系列答案
相关题目