题目内容
【题目】设边长为![]() 的正方形的中心
的正方形的中心![]() 在直线
在直线![]() 上,它的一组对边垂直于直线
上,它的一组对边垂直于直线![]() ,半径为
,半径为![]() 的圆的圆心
的圆的圆心![]() 在直线
在直线![]() 上运动,
上运动,![]() 、
、![]() 两点之间的距离为
两点之间的距离为![]() .
.
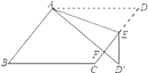
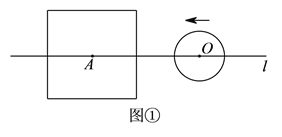
(![]() )如图①,当
)如图①,当![]() 时,填表:
时,填表:
| ⊙ |
|
|
|
|
| __________ |
| __________ |
| __________ |
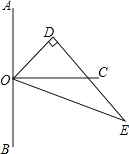
(![]() )如图②,⊙
)如图②,⊙![]() 与正方形有
与正方形有![]() 个公共点
个公共点![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,求此时
,求此时![]() 与
与![]() 之间的数量关系:
之间的数量关系:

(![]() )由(
)由(![]() )可知,
)可知,![]() 、
、![]() 、
、![]() 之间的数量关系和⊙
之间的数量关系和⊙![]() 与正方形的公共点个数密切相关.当
与正方形的公共点个数密切相关.当![]() 时,请根据
时,请根据![]() 、
、![]() 、
、![]() 之间的数量关系,判断⊙
之间的数量关系,判断⊙![]() 与正方形的公共点个数.
与正方形的公共点个数.
(![]() )当
)当![]() 与
与![]() 之间满足(
之间满足(![]() )中的数量关系时,⊙
)中的数量关系时,⊙![]() 与正方形的公共点个数为__________.
与正方形的公共点个数为__________.
【答案】 2 1 0 5
【解析】试题分析:(1)利用圆直线位置关系可得结果.(2) 连接![]() ,在
,在![]() 中,由勾股定理a与r的关系.(3) 当
中,由勾股定理a与r的关系.(3) 当![]() 时,⊙
时,⊙![]() 的直径等于正方形的边长, 与正方形一边相切,相交,与正方形四边形相切,四种情况.(4) 由(
的直径等于正方形的边长, 与正方形一边相切,相交,与正方形四边形相切,四种情况.(4) 由(![]() )中的数易关系,即
)中的数易关系,即![]() ,⊙
,⊙![]() 与正方形的公共点个数为
与正方形的公共点个数为![]() 个.
个.
试题解析:
(![]() )解:当
)解:当![]() 时,
时,![]() 的直径小于正方形的边长,
的直径小于正方形的边长,
![]() 与正方形中垂直于直线
与正方形中垂直于直线![]() 的一边相离、相切、相交,三种情况,
的一边相离、相切、相交,三种情况,
故可确定⊙![]() 与正方形的公共点的个数可能有
与正方形的公共点的个数可能有![]() 、
、![]() 、
、![]() 个.
个.
(![]() )如图所示,连接
)如图所示,连接![]() ,
,
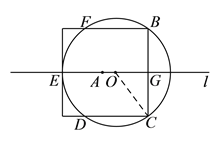
则![]() ,
,![]() ,
,
在![]() 中,由勾股定理得:
中,由勾股定理得:
![]() ,
,
即![]() span>,
span>,
![]() ,
,
![]() ,
,
![]() .
.
(![]() )当
)当![]() 时,⊙
时,⊙![]() 的直径等于正方形的边长,
的直径等于正方形的边长,
此时会出现![]() 与正方形相离,与正方形一边相切,相交,与正方形四边形相切,四种情况,
与正方形相离,与正方形一边相切,相交,与正方形四边形相切,四种情况,
故可确定⊙![]() 与正方形的交点个数可能有
与正方形的交点个数可能有![]() 、
、![]() 、
、![]() 、
、![]() 个.
个.
(![]() )由(
)由(![]() )中的数易关系,
)中的数易关系,
即![]() ,
,
⊙![]() 与正方形的公共点个数为
与正方形的公共点个数为![]() 个.
个.

练习册系列答案
相关题目