题目内容
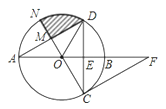
【题目】如图,直线![]() ,点B在直线MN上,点A为直线PQ上一动点,连接AB.在直线AB的上方做
,点B在直线MN上,点A为直线PQ上一动点,连接AB.在直线AB的上方做![]() ,使
,使![]() ,设
,设![]() ,
,![]() 的平分线所在直线交PQ于点D.
的平分线所在直线交PQ于点D.
(1)如图1,若![]() ,且点C恰好落在直线MN上,则
,且点C恰好落在直线MN上,则![]() ________;
________;
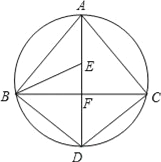
(2)如图2,若![]() ,且点C在直线MN右侧,求
,且点C在直线MN右侧,求![]() 的度数;
的度数;
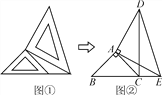
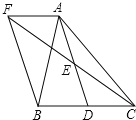
(3)若点C在直线MN的左侧,求![]() 的度数.(用含有α的式子表示)
的度数.(用含有α的式子表示)

【答案】(1)45o;(2) 45o;(3) ![]() .
.
【解析】
(1)证明△ADB是等腰直角三角形即可解决问题.
(2)如图2中,设![]() ,
,![]() .构建方程组即可解决问题.
.构建方程组即可解决问题.
(3)分两种情形:①当点C在直线PQ与MN之间时,设![]() ,
,![]() .②当点C在直线PQ左边时,设
.②当点C在直线PQ左边时,设![]() ,
,![]() .利用平行线的性质、三角形内角和定理、三角形外角性质、四边形内角和定理分别构建方程组即可解决问题.
.利用平行线的性质、三角形内角和定理、三角形外角性质、四边形内角和定理分别构建方程组即可解决问题.
解:(1)如图1中,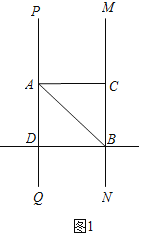
∵PQ∥MN,
∴∠ACB+∠CAD=180°,
∵∠ACB=90°,
∴∠CAD=90°,
∵∠BAC=∠BAQ,
∴∠BAD=45°,
∵DB平分∠CBN,
∴∠DBC=90°,
∵PQ∥MN,
∴∠ADB=90°,
∴∠ABD=45°.
故答案为45°.
(2)根据题意,如图所示,设![]() ,
,![]()
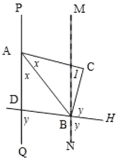
∵![]()
∴![]() ,
, ![]()
∵![]()
∵![]()
∴![]()
∴![]()
(3)①根据题意,如图所示,设![]() ,
,![]()
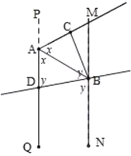
∵![]()
∴![]()
∵![]()
由四边形内角和为![]()
可得![]()
∴![]()
∴![]()
∴![]()
②根据题意,如图所示,设![]() ,
,![]()
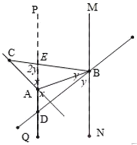
∵![]()
∴![]()
![]()
![]()
在![]() 中
中![]()
![]()
∴![]()
∴![]()
∴![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目