题目内容
【题目】已知:如图,AC⊥BC,CD∥FG,∠1=∠2,试说明:DE⊥AC.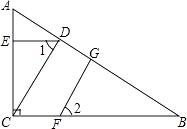
【答案】证明:∵CD∥FG,
∴∠2=∠DCB,
∵∠1=∠2,
∴∠1=∠DCB,
∴DE∥BC,
∵AC⊥BC,
∴DE⊥AC.
【解析】首先依据平行线的性质可证明∠2=∠DCB,然后通过等量代换得∠DCB=∠1,接下来,依据内错角相等两直线平行可得到DE∥BC,最后,依据利用平行线的性质得出结论即可.
【考点精析】关于本题考查的垂线的性质和平行线的判定与性质,需要了解垂线的性质:1、过一点有且只有一条直线与己知直线垂直.2、垂线段最短;由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质才能得出正确答案.

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目