Question

【题目】如图，在Rt△ABC中，D，E为斜边AB上的两个点，且BD=BC，AE=AC，则∠DCE的大小为（度）．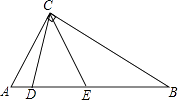

Answer 1

【答案】45
【解析】解：设∠DCE=x，∠ACD=y，则∠ACE=x+y，∠BCE=90°﹣∠ACE=90°﹣x﹣y．

∵AE=AC，

∴∠ACE=∠AEC=x+y，

∵BD=BC，

∴∠BDC=∠BCD=∠BCE+∠DCE=90°﹣x﹣y+x=90°﹣y．

在△DCE中，∵∠DCE+∠CDE+∠DEC=180°，

∴x+（90°﹣y）+（x+y）=180°，

解得x=45°，

∴∠DCE=45°．

故答案为：45．

首先设∠DCE=x，∠ACD=y，则∠ACE=x+y，∠BCE=90°-∠ACE=90°-x-y，然后根据等边对等角的性质可得出∠ACE=∠AEC=x+y，∠BDC=∠BCD=∠BCE+∠DCE=90°-y．接下来，在△DCE中，利用三角形内角和定理列出方程x+（90°-y）+（x+y）=180°，最后，解方程即可求出∠DCE的大小.