题目内容
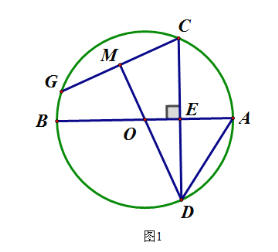
【题目】在Rt△ABC中,∠ABC=90°,∠BAC=30°,将△ABC绕点A顺时针旋转一定的角度![]() 得到△AED,点B、C的对应点分别是E、D.
得到△AED,点B、C的对应点分别是E、D.
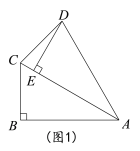
(1)如图1,当点E恰好在AC上时,求∠CDE的度数;
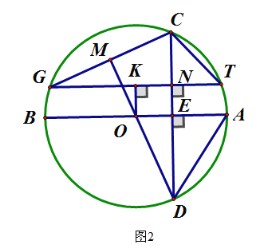
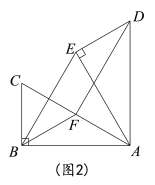
(2)如图2,若![]() =60°时,点F是边AC中点,求证:四边形BFDE是平行四边形.
=60°时,点F是边AC中点,求证:四边形BFDE是平行四边形.


【答案】(1)15°;(2)证明见解析.
【解析】
(1)如图1,利用旋转的性质得CA=DA,∠CAD=∠BAC=30°,∠DEA=∠ABC=90°,再根据等腰三角形的性质求出∠ADC,从而计算出∠CDE的度数;
(2)如图2,利用直角三角形斜边上的中线性质得到BF=![]() AC,利用含30度的直角三角形三边的关系得到BC=
AC,利用含30度的直角三角形三边的关系得到BC=![]() AC,则BF=BC,再根据旋转的性质得到∠BAE=∠CAD=60°,AB=AE,AC=AD ,DE=BC,从而得到DE=BF,△ACD和△BAE为等边三角形,接着由△AFD≌△CBA得到DF=BA,然后根据平行四边形的判定方法得到结论.
AC,则BF=BC,再根据旋转的性质得到∠BAE=∠CAD=60°,AB=AE,AC=AD ,DE=BC,从而得到DE=BF,△ACD和△BAE为等边三角形,接着由△AFD≌△CBA得到DF=BA,然后根据平行四边形的判定方法得到结论.
解:(1)如图1,∵△ABC绕点A顺时针旋转α得到△AED,点E恰好在AC上,
∴CA=CD,∠CAD=∠BAC=30°,∠DEA=∠ABC=90°,
∵CA=DA,
∴∠ACD=∠ADC=![]() (180°30°)=75°,∠ADE=90°-30°=60°,
(180°30°)=75°,∠ADE=90°-30°=60°,
∴∠CDE=75°60°=15°;
(2)证明:如图2,
∵点F是边AC中点,
∴BF=![]() AC,
AC,
∵∠BAC=30°,
∴BC=![]() AC,
AC,
∴BF=BC,
∵△ABC绕点A顺时针旋转60°得到△AED,
∴∠BAE=∠CAD=60°,AB=AE,AC=AD,DE=BC,
∴DE=BF,△ACD和△BAE为等边三角形,
∴BE=AB,
∵点F为△ACD的边AC的中点,
∴DF⊥AC,
易证得△AFD≌△CBA,
∴DF=BA,
∴DF=BE,
而BF=DE,
∴四边形BEDF是平行四边形.

 阅读快车系列答案
阅读快车系列答案