Question

【题目】如图，在平面直角坐标系中，把矩形沿对角线所在的直线折叠，点落在点处，与轴相交于点．矩形的边，的长是关于的一元二次方程的两个根，且．

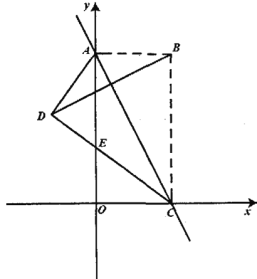
（1）求线段，的长；

（2）求证：，并求出线段的长；

（3）直接写出点的坐标；

（4）若是直线上一个动点，在坐标平面内是否存在点，使以点，，，为顶点的四边形是菱形？若存在，请直接写出点的坐标；若不存在，请说明理由．

Answer 1

【答案】

【解析】

试题分析：（1）解方程即可得到结论；

（2）由四边形ABCO是矩形，得到AB=OC，∠ABC=∠AOC=90°，根据折叠的性质得到AD=AB，∠ADE=∠ABC=90°，根据全等三角形的判定得到△ADE≌△COE；根据勾股定理得到OE=3；

（3）过D作DM⊥x轴于M，则OE∥DM，根据相似三角形的性质得到CM=，DM=，于是得到结论．

（4）过P1作P1H⊥AO于H，根据菱形的性质得到P1E=CE=5，P1E∥AC，设P1H=k，HE=2k，根据勾股定理得到P1E= k=5，于是得到P1（﹣，2+3），同理P3（，3﹣2），当A与F重合时，得到P2（4，5）；当CE是菱形EP4CF4的对角线时，四边形EP4CF4是菱形，得到EP4=5，EP4∥AC，如图2，过P4作P4G⊥x轴于G，过P4作P4N⊥OE于N，根据勾股定理即可得到结论．

试题解析：（1）解方程x2﹣12x+32=0得，x1=8，x2=4，∵OA＞OC，∴OA=8，OC=4；

（2）∵四边形ABCO是矩形，∴AB=OC，∠ABC=∠AOC=90°，

∵把矩形OABC沿对角线AC所在直线折叠，点B落在点D处，∴AD=AB，∠ADE=∠ABC=90°，

∴AD=OC，∠ADE=∠COE，在△ADE与△COE中， ，∴△ADE≌△COE；

∵CE2=OE2+OC2，即（8﹣OE）2=OE2+42，∴OE=3；

（3）过D作DM⊥x轴于M，则OE∥DM，

∴△OCE∽△MCD，∴ ，∴CM=，DM=，∴OM= ，

∴D（﹣，）；

（4）存在；∵OE=3，OC=4，∴CE=5，过P1作P1H⊥AO于H，∵四边形P1ECF1是菱形，∴P1E=CE=5，P1E∥AC，

∴∠P1EH=∠OAC，∴ = ，∴设P1H=k，HE=2k，∴P1E=k=5，∴P1H=，HE=2，

∴OH=2+3，∴P1（﹣，2+3），同理P3（，3﹣2），

当A与F重合时，四边形F2ECP2是菱形，∴EF2∥CP2，EF2，=CP2=5，∴P2（4，5）；

当CE是菱形EP4CF4的对角线时，四边形EP4CF4是菱形，∴EP4=5，EP4∥AC，

如图2，过P4作P4G⊥x轴于G，过P4作P4N⊥OE于N，则P4N=OG，P4G=ON，EP4∥AC，∴=，

设P4N=x，EN=2x，∴P4E=CP4=x，∴P4G=ON=3﹣2x，CG=4﹣x，∴（3﹣2x）2+（4﹣x）2=（x）2，

∴x= ，∴3﹣2x= ，∴P4（，），

综上所述：存在以点E，C，P，F为顶点的四边形是菱形，P（﹣，2+3），（，3﹣2），（4，5），（，）．