题目内容
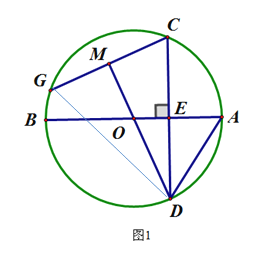
【题目】如图，AB为⊙O的直径，弦CD⊥AB于点E，G为⊙O一点，连接OD, 并延长DO交CG于点M，CM=GM.
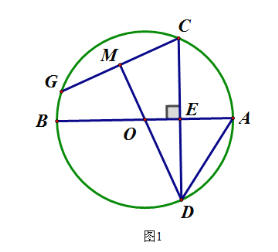
（1）求证：∠GCD=2∠ADC
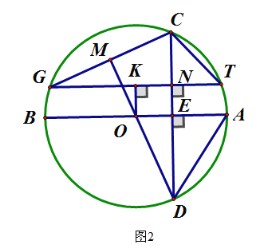
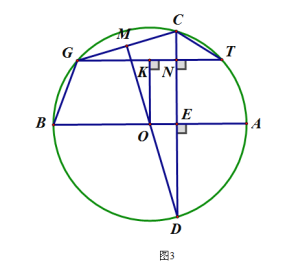
（2）过点G作GN⊥CD，交CD于点N,交⊙O于点T，过点O作OK⊥TG，交TG于点K,连接TC,求证：TC=2NK
（3）在（2）的条件下，连接BG，BG=11，CD=30，求sin∠CTN.
【答案】（1）详见解析；（2）详见解析；（3）
【解析】
（1）利用垂径定理，等弧所对的圆周角相等进行证明；
（2）连接PC,利用垂径定理，三角形中位线的性质，矩形的判定和性质进行证明；
（3）连接BC、BD，过点D作DH⊥BC垂足为H，过点D作DF垂直于GB的延长线于F，利用垂径定理，等弧所对的圆周角相等先证明
，再证
，然后设
，再利用双勾股
列出方程，求得
，再设
，则
，再利用勾股定理得
，解得
,最后利用
解得
.
解：（1）
连接
∵
∴
∴∠CGD=2∠ADC
又∵连接OD并延长DO交CG于点M，且CM=GM
∴DM⊥GC
∴DC=DG
∴∠GCD=∠CGD =2∠ADC
（2）
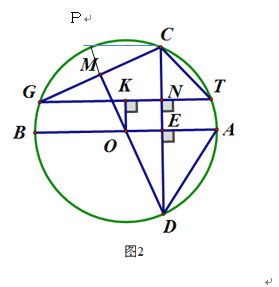
延长DM交圆O于点P,连接PC
∵CM=GM.且DM经过点O
∴DP⊥CG，∠PCD=90°
又∵CD⊥GT,OK⊥GT,CD⊥AB
∴四边形KNEO是矩形
∴KN=OE,OE∥GT∥PC,
∵
∴
∴
,OE=
=NK
∴
∵
都是中点
∴
∴TC=2NK
（3）连接BC、BD，过点D作DH⊥BC垂足为H，过点D作DF垂直于GB的延长线于F
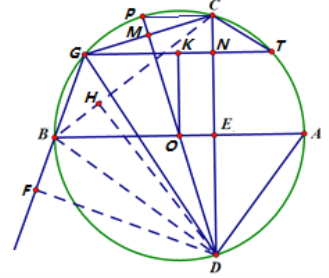
∵AB为⊙O的直径，且CD⊥AB
∴
∵CM=GM 且DP⊥CG
∴
又∵
∴
∴
∴
∴
设
则
∴
则
解得
或
（不符合题意，舍去）
∴
∴
设，则
∴
解得：
∴
∴
∴
∴
∵
∴
∴
练习册系列答案
相关题目
