题目内容
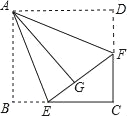
【题目】如图,Rt△ABC中,∠ACB=90°,AC=16,BC=4,D为AB上一点,DE⊥AC于点E,DE=1,P为CE上一动点,设CP的长为a.
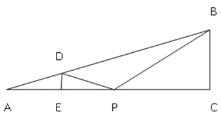
(1)求CE的长;
(2)a为何值时,△DEP与△BCP相似?
(3)当PD+PB有最小值时,求a的值及最小值.
【答案】(1)CE=12;(2)a的值为![]() 或6+4
或6+4![]() 或6-
或6-![]() ;(3)13.
;(3)13.
【解析】
(1)证明三角形ADE与三角形ABC相似,根据对应边成比例![]() ,且AE=16-CE,可解得CE的值.
,且AE=16-CE,可解得CE的值.
(2)此时分为两种情况进行谈论,分别是△DEP∽△BCP与△DEP∽△PCB.
(3)找到B点关于AC的对称点F,当D与F在同一直线上时,PD+PB最短.
(1)∵DE⊥AC ∠AED=90°=∠ACB 又∠A公共
∴△ADE∽△ABC ∴![]() 即
即![]() ,CE=12.
,CE=12.
(2)分两种情况:①△DEP∽△BCP,此时![]() ,即
,即![]() ,a=
,a=![]()
②△DEP∽△PCB,此时![]() ,即
,即![]() ,
,![]() ,
,![]()
∴a的值为![]() 或6+4
或6+4![]() 或6-
或6-![]() .
.
(3)
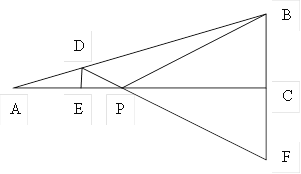
延长BC至点F,使CF=CB,连接DF交CE于点P,如图:
∠DPE=∠CPF,∠DEP=∠PCF,则△DEP∽△FCP
于是![]() ,得 a=
,得 a=![]() .
.
此时BP=![]() ,DP=
,DP=![]() ,最小值为13.
,最小值为13.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目