题目内容
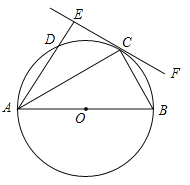
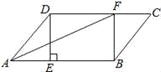
【题目】如图，在ABCD中，过点D作DE⊥AB于点E，点F在边CD上，CF=AE，连接AF，BF.
(1)求证：四边形BFDE是矩形；
(2)已知∠DAB=60°，AF是∠DAB的平分线，若AD=3，求DC的长度.
【答案】(1)证明见解析；(2)CD=
.
【解析】
（1）由题意可证四边形DFBE是平行四边形，且DE⊥AB，可得结论;（2）根据直角三角形的边角关系可求DE的长度，则可得BF的长度，即可求CD的长度．
证明(1)∵四边形ABCD是平行四边形，
∴DC∥AB，DC=AB，
∵CF=AE
∴DF=BE且DC∥AB，
∴四边形DFBE是平行四边形，
又∵DE⊥AB，
∴四边形DFBE是矩形.
(2)∵∠DAB=60°，AD=3，DE⊥AB，
∴AE=
，DE=
AE=
∵四边形DFBE是矩形
∴BF=DE=
∵AF平分∠DAB
∴∠FAB=
∠DAB=30°，且BF⊥AB
∴AB=BF=
∴CD=
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
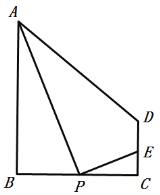
【题目】如图，在梯形
中，
，
，
，
．P为线段
上的一动点，且和B、C不重合，连接
，过点P作
交射线
于点E．
聪聪根据学习函数的经验，对这个问题进行了研究：
（1）通过推理，他发现
，请你帮他完成证明．
（2）利用几何画板，他改变的长度，运动点P，得到不同位置时，
、
的长度的对应值：
当
时，得表1：
| … | 1 | 2 | 3 | 4 | 5 | … |
| … | 0.83 | 1.33 | 1.50 | 1.33 | 0.83 | … |
当
时，得表2：
| … | 1 | 2 | 3 | 4 | 5 | 6 | 7 | … |
| … | 1.17 | 2.00 | 2.50 | 2.67 | 2.50 | 2.00 | 1.17 | … |
这说明，点P在线段上运动时，要保证点E总在线段上，
的长度应有一定的限制．
①填空：根据函数的定义，我们可以确定，在和的长度这两个变量中，_____的长度为自变量，_____的长度为因变量；
②设
，当点P在线段上运动时，点E总在线段上，求m的取值范围．
