ЬтФПФкШн
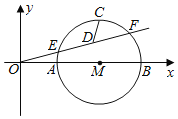
ЁОЬтФПЁПвбжЊЖўДЮКЏЪ§yЃНax2Љ2xЃЋ3ОЙ§ЕуA(Љ3ЃЌ0)ЃЌPЪЧХзЮяЯпЩЯЕФвЛИіЖЏЕуЃЎ
ЃЈ1ЃЉЧѓИУКЏЪ§ЕФБэДяЪНЃЛ
ЃЈ2ЃЉШчЭМЫљЪОЃЌЕуPЪЧХзЮяЯпЩЯдкЕкЖўЯѓЯоФкЕФвЛИіЖЏЕуЃЌЧвЕуPЕФКсзјБъЮЊtЃЌСЌНгACЃЌPAЃЌPCЃЎЧѓЁїACPЕФУцЛ§SЙигкtЕФКЏЪ§ЙиЯЕЪНЃЌВЂЧѓГіЁїACPЕФУцЛ§зюДѓЪБЕуPЕФзјБъЃЎ
ЃЈ3ЃЉСЌНгBCЃЌдкХзЮяЯпЩЯЪЧЗёДцдкЕуPЃЌЪЙЕУЁЯPCAЃНЁЯOCBЃПШєДцдкЃЌЧѓГіЕуPЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ

ЁОД№АИЁПЃЈ1ЃЉyЃНЃx2Ѓ2xЃЋ3ЃЛЃЈ2ЃЉ![]() ЃЌ
ЃЌ![]() ЃЛЃЈ3ЃЉ
ЃЛЃЈ3ЃЉ![]() Лђ(Ѓ4ЃЌЃ5)
Лђ(Ѓ4ЃЌЃ5)
ЁОНтЮіЁП
ЃЈ1ЃЉНЋЕуA(-3ЃЌ0)ДјШыНтЮіЪНЧѓНтМДПЩЃЛ
ЃЈ2ЃЉЙ§ЕуPзіДЙЯпЃЌдђ![]() ЃЌРћгУвбжЊAЁЂCЕузјБъПЩвдЧѓГіACжБЯпЕФНтЮіЪНЃЌДгЖјЕШЕНPЁЂQСНЕузјБъЃЌдйРћгУШ§НЧаЮУцЛ§ЙЋЪНЧѓНтМДПЩЃЛ
ЃЌРћгУвбжЊAЁЂCЕузјБъПЩвдЧѓГіACжБЯпЕФНтЮіЪНЃЌДгЖјЕШЕНPЁЂQСНЕузјБъЃЌдйРћгУШ§НЧаЮУцЛ§ЙЋЪНЧѓНтМДПЩЃЛ
ЃЈ3ЃЉзіГіИЈжњЯпЃЌНшжњШ§НЧКЏЪ§ЕУЕНЁЯPCAЃНЁЯOCBЕФЙиЯЕЃЌДгЖјЕУЕНБпгыБпЕФЙиЯЕЃЌЧѓНтГіЮДжЊЪ§ЃЎ
ЃЈ1ЃЉЖўДЮКЏЪ§![]() Й§ЕуA(-3ЃЌ0)ЃЌДњШыга0=9a+6+3ЃЌa=-1ЃЌ
Й§ЕуA(-3ЃЌ0)ЃЌДњШыга0=9a+6+3ЃЌa=-1ЃЌ
ЙЪЮЊДЫКЏЪ§НтЮіЪНЮЊ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЙ§ЕуPзїPN![]() AOгкЕуNЃЌНЛACгкЕуQЃЌ
AOгкЕуNЃЌНЛACгкЕуQЃЌ
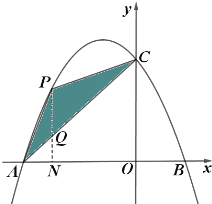
гЩЃЈ1ЃЉжЊЃЌC(0ЃЌ3)ЃЌЩшжБЯпACЕФНтЮіЪНЮЊy=kx+bЃЌЃЈk![]() 0ЃЉЃЌНЋA(-3ЃЌ0)ЁЂC(0ЃЌ3)ДњШыy=kx+bЃЌЕУ
0ЃЉЃЌНЋA(-3ЃЌ0)ЁЂC(0ЃЌ3)ДњШыy=kx+bЃЌЕУ![]() НтЕУ
НтЕУ![]() ЃЌ
ЃЌ
ЁржБЯпACЕФНтЮіЪНЮЊy=x+3ЃЌ
ЁпЕуPдкХзЮяЯп![]() ЩЯЃЌЕуQдкжБЯпACЩЯЃЌ
ЩЯЃЌЕуQдкжБЯпACЩЯЃЌ
ЁрP(tЃЌ![]() )ЃЌQ(tЃЌt+3)ЃЌ
)ЃЌQ(tЃЌt+3)ЃЌ
ЁрPQ=![]() =
=![]() ЃЌ
ЃЌ
![]() ЃЛ
ЃЛ
ЕБ![]() ЪБЃЌЁїACPЕФУцЛ§зюДѓЃЌ
ЪБЃЌЁїACPЕФУцЛ§зюДѓЃЌ![]() ЃЛ
ЃЛ
ЙЪSЙигкtЕФКЏЪ§ЙиЯЕЪН![]() ЃЌP
ЃЌP![]() ЃЛ
ЃЛ
ЃЈ3ЃЉХзЮяЯпЩЯДцдкЕуPЃЌЪЙЕУЁЯPCAЃНЁЯOCBЃЌ
Й§PЕузїPD![]() ACЃЌНЛACгкЕуDЃЌШчЭМ
ACЃЌНЛACгкЕуDЃЌШчЭМ
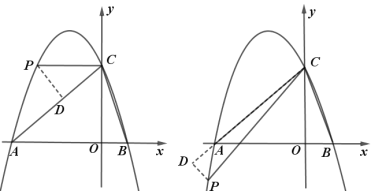
вбжЊХзЮяЯпЗНГЬЮЊ![]() ЃЌ
ЃЌ![]() ЃЌx=1ЃЌМДПЩЕУЕНB(1ЃЌ0)ЃЌ
ЃЌx=1ЃЌМДПЩЕУЕНB(1ЃЌ0)ЃЌ
дђгаOB=1ЃЌOC=3ЃЌ![]() ЃЌ
ЃЌ
ЕуPдкХзЮяЯпЩЯЃЌЩшЕуP(aЃЌ![]() )ЃЌжБЯпACЃКy=x+3ЃЌдђ
)ЃЌжБЯпACЃКy=x+3ЃЌдђ![]() ЃЌжБЯпPDЙ§ЕуPЃЌМДПЩЧѓГіPDЕФНтЮіЪНЮЊ
ЃЌжБЯпPDЙ§ЕуPЃЌМДПЩЧѓГіPDЕФНтЮіЪНЮЊ![]() ЃЌгжвђЮЊDЮЊPDгыACЕФНЛЕуЃЌСЊСЂЗНГЬзщга
ЃЌгжвђЮЊDЮЊPDгыACЕФНЛЕуЃЌСЊСЂЗНГЬзщга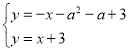 ЃЌНтЕУга
ЃЌНтЕУга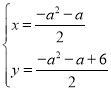 ЃЌМДD(
ЃЌМДD(![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
ЁпЁЯPCAЃНЁЯOCBЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр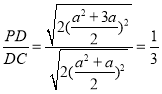 ЃЌНтЕУa=-4Лђa=
ЃЌНтЕУa=-4Лђa=![]() ЃЌ
ЃЌ
ЫљвдДцдкЕуP(-4ЃЌ-5)Лђ![]() ЃЎ
ЃЎ

 гфПьЕФКЎМйФЯОЉГіАцЩчЯЕСаД№АИ
гфПьЕФКЎМйФЯОЉГіАцЩчЯЕСаД№АИ