��Ŀ����
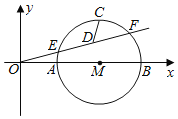
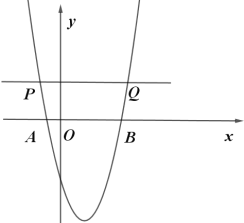
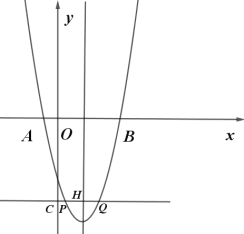
����Ŀ����ͼ����֪���κ���y��ax2��bx��5��a��b�dz�����a![]() 0����ͼ����x�ύ�ڵ�A����1��0���͵�B��5��0������ֱ��y��t��tΪ�������������߽��ڲ�ͬ������P��Q����P��Q����ࣩ��
0����ͼ����x�ύ�ڵ�A����1��0���͵�B��5��0������ֱ��y��t��tΪ�������������߽��ڲ�ͬ������P��Q����P��Q����ࣩ��
��1���������ߵĽ���ʽ��
��2����ֱ��y��t��y�ύ�ڵ�C����CQ=3CP����t��ֵ��
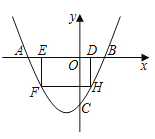
��3����������y��ax2��bx��5��x���·��IJ�����x�ᷭ�ۣ�����ֱ��y��t�뷭�ۺ��ͼ���ڵ�M��N����M��N�ܷ����߶�PQ�����ȷֵ㣿���ܣ���PQ�ij��ȣ������ܣ���˵�����ɣ�
���𰸡���1��![]() ����2��-8��7����3���ܣ�
����2��-8��7����3���ܣ�![]()
��������
��1������A����B��������������ߣ��ⷽ���鼴����������߽���ʽ��
��2����y��t��x����Ϸ�����x���·����ֽ������ۣ����������ߵĶԳ��Ժ�CQ=3CP���������P����Q�ĺ����꣬����Q��������������������t��ֵ��
��3�����ݶԳ��Կɵ÷��ۺ�������ߵĽ���ʽ���ٸ��ݵ�P����Q��ֱ��y=t��������![]() ����M����N��������
����M����N��������![]() �Ľ��㣬�������̣���õ�P��Q��M��N�����꣬�����õ�M��N���߶�PQ�����ȷֵ㣬�ó�PM=MN=NQ���ݴ����t��ֵ����������߶�PQ�ij���
�Ľ��㣬�������̣���õ�P��Q��M��N�����꣬�����õ�M��N���߶�PQ�����ȷֵ㣬�ó�PM=MN=NQ���ݴ����t��ֵ����������߶�PQ�ij���
�⣺��1����A����1��0����B��5��0�����������ϣ�
��![]() ����ã�
����ã�![]() ��
��
����κ�����ϵʽΪy��x2��4 x��5��
��2����y��t��x����Ϸ�����ͼ��
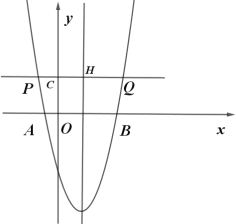
�����ߵĶԳ���![]() ����ֱ��y��t���ڵ�H��
����ֱ��y��t���ڵ�H��
��CH=2��
���������ߵĶԳ��Կɵã�PH=QH��
��CQ=3CP��
��PH=CH=2��QH=2CH=4��
��CQ=6��
���Q������Ϊ![]() ��
��
�ߵ�Q��������y��x2��4 x��5�ϣ�����ã�
![]() ��
��
��y��t��x����Ϸ�����ͼ��
��ʱ�����������ߵĶԳ��Կɵã�
CH=HQ��
��CQ=3CP��
��CP=PH=1��HQ=2CP=2��
���P������Ϊ![]() ��
��
�ߵ�P��������y��x2��4 x��5�ϣ�����ã�
![]() ��
��
����������t��![]() ��7 ��
��7 ��
��3����M��N�������߶�PQ�����ȷֵ㣬��ʱ![]() ��
��
������![]() �Ķ�������Ϊ
�Ķ�������Ϊ![]() ��
��
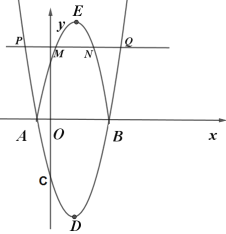
��������y��ax2��bx��5��x���·��IJ�����x�ᷭ�ۣ�
���E���D����x��Գƣ���E������Ϊ![]() ��
��
�෭�ۺ�������߽���ʽΪ��![]() ��
��
��ֱ��y=t��������![]() ����P��Q���㣬
����P��Q���㣬
��![]() ����ã�
����ã�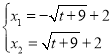 ��
��
���P������Ϊ![]() ����Q������Ϊ
����Q������Ϊ![]() ��
��
��ֱ��y=t��������![]() ����M��N���㣬
����M��N���㣬
��![]() ����ã�
����ã�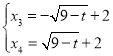 ,
,
���M������Ϊ![]() ����N������Ϊ
����N������Ϊ![]() ��
��
Ҫʹ��M��N���߶�PQ�����ȷֵ㣬��PM=MN=NQ��
![]() ��
��
��ã�![]() ��
��
��![]() ,
,