��Ŀ����
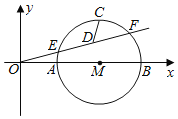
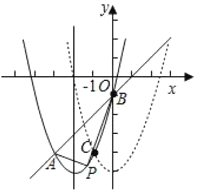
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪������![]() ��ֱ��AB�ཻ��A��B���㣬����
��ֱ��AB�ཻ��A��B���㣬����![]() ��
��![]() ��
��
��1����������ߵĺ�������ʽ��
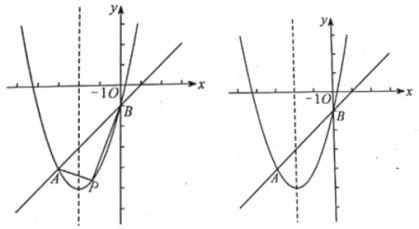
��2����PΪֱ��AB�·��������ϵ�����һ�㣬����PA��PB����![]() ��������ֵ��
��������ֵ��
��3����������������ƽ��2����λ���ȵõ�������![]() ��ƽ�ƺ����������ԭ�������ཻ�ڵ�C����DΪԭ�����߶Գ����ϵ�һ�㣬��ƽ��ֱ������ϵ���Ƿ���ڵ�E��ʹ�Ե�B��C��D��EΪ������ı���Ϊ���Σ������ڣ���ֱ��д����E�����ꣻ�������ڣ���˵�����ɣ�
��ƽ�ƺ����������ԭ�������ཻ�ڵ�C����DΪԭ�����߶Գ����ϵ�һ�㣬��ƽ��ֱ������ϵ���Ƿ���ڵ�E��ʹ�Ե�B��C��D��EΪ������ı���Ϊ���Σ������ڣ���ֱ��д����E�����ꣻ�������ڣ���˵�����ɣ�
���𰸡���1��![]() ����2��
����2��![]() ������ֵΪ
������ֵΪ![]() ����3�����ڣ�
����3�����ڣ�![]()
��������
��1������A��B��������������߱���ʽ��������⣻
��2����![]() ����ý���ʽ������P��x��ô�����ֱ��AB���ڵ�F�����
����ý���ʽ������P��x��ô�����ֱ��AB���ڵ�F�����![]() ����
����![]() ��
��![]()
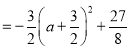 ��������⣻
��������⣻
��3����BCΪ���εıߡ����εĵĶԽ�������������ֱ���⼴�ɣ�
�⣺��1���������߹�![]() ��
��![]()
��![]()
��![]()
��![]()
��2����![]() ������
������![]()
![]() ����
����![]()
��![]()
����P��x��ô�����ֱ��AB���ڵ�F
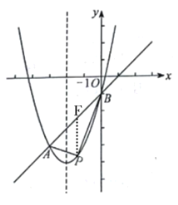
���![]() ����
����![]()
��Ǧ�������ɵ�
![]()
![]()
![]()
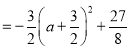
��![]() ������ֵΪ
������ֵΪ![]()
��3����3�������ߵı���ʽΪ��y��x2��4x1����x��2��25��
��ƽ�ƺ�������߱���ʽΪ��y��x25��
����������ʽ����ã�![]() ���ʵ�C��1��4����
���ʵ�C��1��4����
���D��2��m������E��s��t��������B��C������ֱ�Ϊ��0��1������1��4����
�ٵ�BCΪ���εı�ʱ��
��C����ƽ��1����λ����ƽ��3����λ�õ�B��ͬ��D��E������ƽ��1����λ����ƽ��3����λ�õ�E��D����
��2��1��s��m��3��t�ٻ�21��s��m3��t�ڣ�
����D��E���·�ʱ����BE��BC����s2����t��1��2��12��32�ۣ�
����D��E���Ϸ�ʱ����BD��BC����22����m��1��2��12��32�ܣ�
�����٢۲���ã�s��1��t��2��4����ȥ4�����ʵ�E��1��2����
�����ڢܲ���ã�s��-3��t��-4��![]() ���ʵ�E��-3��-4��
���ʵ�E��-3��-4��![]() ����-3��-4
����-3��-4![]() ����
����
�ڵ�BCΪ���εĵĶԽ���ʱ��
�����е㹫ʽ�ã�1��s2��41��m��t�ݣ�
��ʱ��BD��BE����22����m��1��2��s2����t��1��2�ޣ�
�����ݢ���ã�s��1��t��3��
�ʵ�E��1��3����
���ϣ���E������Ϊ����1��2����![]() ��
��![]() ��1��3����
��1��3����
����ڣ�![]()