Question

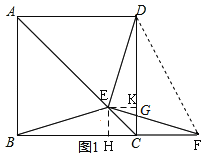
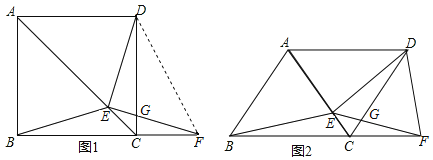
【题目】如图1，在正方形中，是对角线上的一点，点在的延长线上，交于，．

（1）求证：；

（2）连接，若，求；

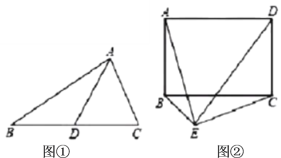
（3）如图2，若把正方形改为菱形，其他条件不变，当时，猜想与的数量关系，并证明你的猜想．

Answer 1

【答案】（1）证明见解析；（2）BE＝；（3）BE＝DF，理由见解析

【解析】

（1）根据正方形的性质证明△BCE≌△DCE即可；

（2）过E作EK⊥DC于K，EH⊥BC于H，构建正方形EHCK，通过证明Rt△DEK≌Rt△FEH得出△DEF是等腰直角三角形，进而得解；

（3）先证明△BCE≌△DCE，得∠EBC＝∠EDC，BE＝ED，根据三角形内角和可得∠DEF＝∠DCF＝∠ABC＝60°，进而得出△DEF是等边三角形，可得结论．

（1）证明：∵四边形ABCD是正方形，

∴BC＝DC，∠BCE＝∠DCE，

∵EC＝EC，

∴△BCE≌△DCE，

∴BE＝ED，

∵EF＝ED，

∴EB＝EF；

（2）解：如图1，过E作EK⊥DC于K，EH⊥BC于H，

∴∠EKC＝∠EHC＝∠BCD＝90°，

∴四边形EHCK是矩形，

∵∠ECH＝45°，

∴△EHC是等腰直角三角形，

∴EH＝CH，

∴矩形EHCK是正方形，

∴EK＝EH，

∴Rt△DEK≌Rt△FEH，

∴∠DEK＝∠FEH，

∴∠DEK+∠FEK＝∠FEH+∠FEK，

∴∠DEF＝90°，

∴△DEF是等腰直角三角形，

∵DF＝2，

∴DE＝，

∴BE＝；

（3）解：BE＝DF，理由是：

∵四边形ABCD是菱形，

∴BC＝DC，∠BCE＝∠DCE，

∵EC＝EC，

∴△BCE≌△DCE，

∴∠EBC＝∠EDC，BE＝ED，

∵EF＝ED，

∴EB＝EF，

∴∠EBC＝∠EFC，

∴∠EDC＝∠EFC，

∵∠EGD＝∠CGF，

∴∠DEF＝∠DCF＝∠ABC＝60°，

∴△DEF是等边三角形，

∴DF＝EF，

∴BE＝DF．