Question

【题目】如图，过点P作PA，PB，分别与以OA为半径的半圆切于A，B，延长AO交切线PB于点C，交半圆与于点D．

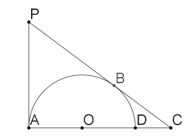
（1）若PC=5，AC=4，求BC的长；

（2）设DC:AD=1:2，求的值．

Answer 1

【答案】（1）BC=2；（2）3

【解析】

（1）由切线的性质可得PA=PB，∠PAC=90°，由勾股定理可求AP=3，即可求BC的长；

（2）由题意可得CD=OD=OB，可证△OBC∽△PAC，可得PC=2PA，即可求解．

（1）∵PA，PB是⊙O的切线，∴PA=PB，∠PAC=90°，∴AP3，∴PB=AP=3，∴BC=PC﹣PB=2．

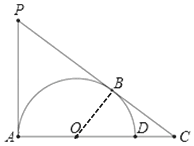
（2）连接OB．

∵CD：AD=1：2，AD=2OD，∴CD=OD=OB，∴CO=2OB．

∵PB是⊙O切线，∴OB⊥PC，∴∠OBC=90°=∠PAC，且∠C=∠C，∴△OBC∽△PAC，∴，∴PC=2PA，∴．