题目内容
【题目】小李在学习了定理“直角三角形斜边上的中线等于斜边的一半”之后做了如下思考,请你帮他完成如下问题:
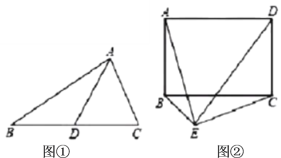
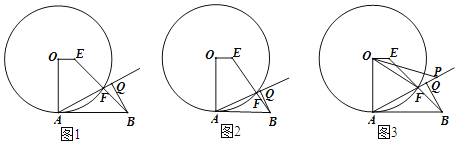
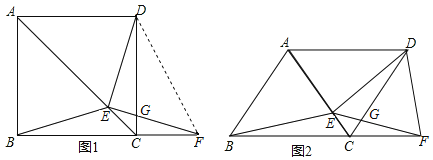
(1)他认为该定理有逆定理:“如果一个三角形某条边上的中线等于该边长的一半,那么这个三角形是直角三角形”应该成立.即如图①,在![]() 中,
中,![]() 是
是![]() 边上的中线,若
边上的中线,若![]() ,求证:
,求证:![]() .
.
(2)如图②,已知矩形![]() ,如果在矩形外存在一点
,如果在矩形外存在一点![]() ,使得
,使得![]() ,求证:
,求证:![]() .(可以直接用第(1)问的结论)
.(可以直接用第(1)问的结论)
(3)在第(2)问的条件下,如果![]() 恰好是等边三角形,请求出此时矩形的两条邻边
恰好是等边三角形,请求出此时矩形的两条邻边![]() 与
与![]() 的数量关系.
的数量关系.
【答案】(1)详见解析;(2)详见解析;(3)![]()
【解析】
(1)利用等腰三角形的性质和三角形内角和即可得出结论;
(2)先判断出OE=![]() AC,即可得出OE=
AC,即可得出OE=![]() BD,即可得出结论;
BD,即可得出结论;
(3)先判断出△ABE是底角是30°的等腰三角形,即可构造直角三角形即可得出结论.
(1)∵AD=BD,
∴∠B=∠BAD,
∵AD=CD,
∴∠C=∠CAD,
在△ABC中,∠B+∠C+∠BAC=180°,
∴∠B+∠C+∠BAD+∠CAD=∠B+∠C+∠B+∠C=180°
∴∠B+∠C=90°,
∴∠BAC=90°,
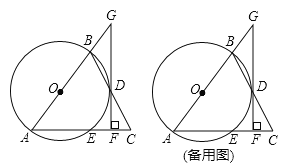
(2)如图②,连接![]() 与
与![]() ,交点为
,交点为![]() ,连接
,连接![]()
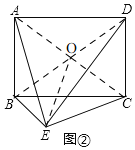
![]() 四边形
四边形![]() 是矩形
是矩形
![]()
![]()
![]()
![]()
![]()
![]()
![]()
(3)如图3,过点![]() 做
做![]() 于点
于点![]()

![]() 四边形
四边形![]() 是矩形
是矩形
![]() ,
,![]()
![]() 是等边三角形
是等边三角形
![]() ,
,![]()
由(2)知,![]()
![]()
![]()
![]() 在
在![]() 中,
中,![]()
![]() ,
,![]()
![]()
![]()
![]()

练习册系列答案
相关题目