题目内容
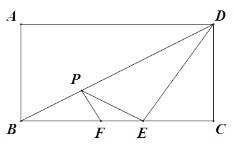
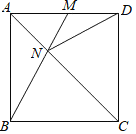
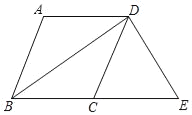
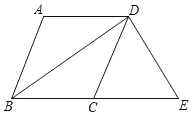
【题目】如图,在四边形ABCD中,AD∥BC,BA=BC,BD平分∠ABC.
(1)求证:四边形ABCD是菱形;
(2)过点D作DE⊥BD,交BC的延长线于点E,若BC=5,BD=8,求四边形ABED的周长.
【答案】(1)详见解析;(2)26.
【解析】
(1)根据平行线的性质得到∠ADB=∠CBD,根据角平分线定义得到∠ABD=∠CBD,等量代换得到∠ADB=∠ABD,根据等腰三角形的判定定理得到AD=AB,根据菱形的判定即可得到结论;
(2)由垂直的定义得到∠BDE=90°,等量代换得到∠CDE=∠E,根据等腰三角形的判定得到CD=CE=BC,根据勾股定理得到DE=![]() =6,于是得到结论.
=6,于是得到结论.
(1)证明:∵AD∥BC,
∴∠ADB=∠CBD,
∵BD平分∠ABC,
∴∠ABD=∠CBD,
∴∠ADB=∠ABD,
∴AD=AB,
∵BA=BC,
∴AD=BC,
∴四边形ABCD是平行四边形,
∵BA=BC,
∴四边形ABCD是菱形;
(2)解:∵DE⊥BD,
∴∠BDE=90°,
∴∠DBC+∠E=∠BDC+∠CDE=90°,
∵CB=CD,
∴∠DBC=∠BDC,
∴∠CDE=∠E,
∴CD=CE=BC,
∴BE=2BC=10,
∵BD=8,
∴DE=![]() =6,
=6,
∵四边形ABCD是菱形,
∴AD=AB=BC=5,
∴四边形ABED的周长=AD+AB+BE+DE=26.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目