Question

【题目】如图，等边△ABC中，AB=6，D是AC的中点，E是BC延长线上的一点，CE=CD，DF⊥BE，垂足为F．

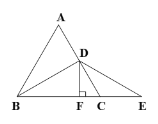
（1）求证：BF=EF；

（2）求△BDE的面积．

Answer 1

【答案】（1）见解析；（2）

【解析】

（1）先证△BDE为等腰三角形，依据等腰三角形的性质，即可得到BF=EF；

（2）先求得BE=BC+CE=9，再根据∠DBE=30°，DB=3，即可得出DF=，进而得到△BDE的面积．

解：（1）∵△ABC为等边三角形，D为AC中点，

∴∠CBD=30°，∠ACB=60°，

又∵CD=CE，

∴∠CDE=∠CED=30°，

∴BD=DE，则△BDE为等腰三角形，

∵DF⊥BE，

∴BF=EF；

（2）∵△ABC为等边三角形，D为AC中点，AB=6，

∴AD=CD，CE=CD，∠DBC=，

∴CE=CD=3，

∴BE=BC+CE=9，

∴，

∴DF=，

S△BDE==，

故答案为：.